Example to Understand Finite Automata

For Complete YouTube Video: Click Here

In this class, We discuss an example to understand finite automata.

This reader should have prior knowledge of Introduction to Formal languages and Automata Theory. Click here.

First, refresh the concept discussed in the previous class and continue with our example.

The example considered from our previous class is the string 100111.

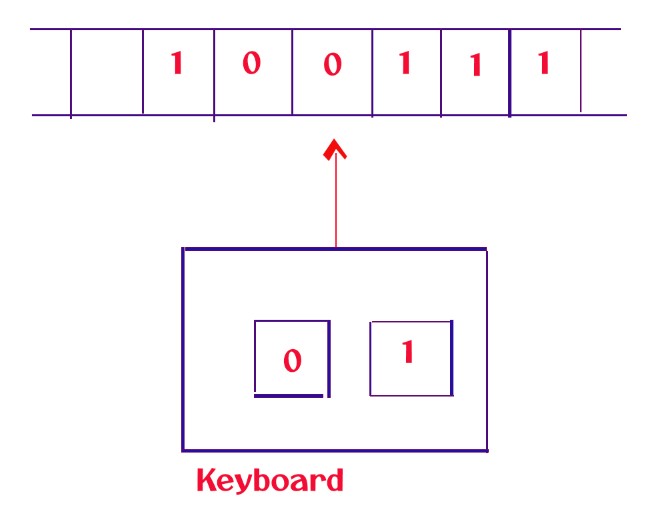
Logic: We need to identify strings that contain the last character ‘1’.

The input entered will be saved in RAM.

We move on the memory till the last character and check the character is ‘1’.

This class will construct a logic to identify the strings containing last character ‘1’ if our device does not have memory.

If memory is not present, we need to remember three points to construct the logic.

The first point is to take the first character and process immediately, then take the second character and process and so on.

Immediately after taking the character, we have to process because we do not have a memory to save.

The second point, we do not know what character comes next. So logic should depend on the present input.

Third Point, We do not know the length of the string because we are not saving the input in memory.

Based on the above three points, we need to identify The logic.

Just follow the procedure given below. In the end, the reader will get clarity on how to write logic without memory location.

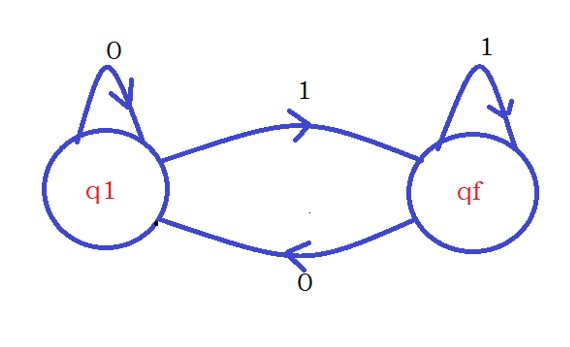
In our example, we consider two states, q1 and qf.

The state q1 is the initial state. Our logic starts from the initial state.

The state qf is the final state.

The states are shown above.

Our objective is to move on the states as we read the input string.

How to move on states will be explained below.

Logic:

The first point, after processing input, if we end up in the final state, the input string is accepted.

Second point, If we end up in other than the final state, the input is not accepted.

Based on the points mentioned above, we need to think of the logic.

The below example shows the reader step by step process of how to think the logic.

The example takes the input string 100111.

First step: we start at the initial state q1.

The first input character is taken. The input is ‘1’.

Assume if this is the final character. The string ‘1’ should be accepted because the string has the last character ‘1’.

We move from state q1 to qf. It is shown in the below diagram.

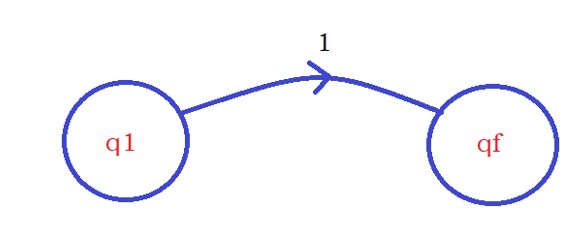
Second step: Know we are at state qf. Take the next input.

The next input character is ‘0’. On qf state, when we see the input ‘0’, we move to the state q1.

We move to state q1, because if the present input character is the last. We should not end up in the final state.

On seeing the input character zero on the state qf, we move to the state q1.

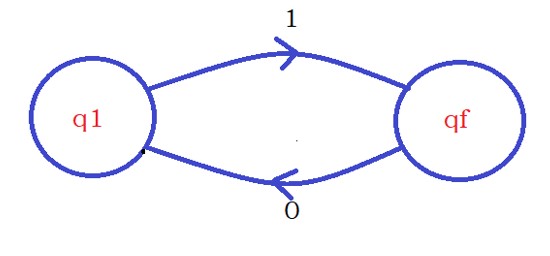
Third step: Know we are in state q1. The following input character we see is ‘0’.

Assume if the character ‘0’ is the last. We should not end up on qf. so we stay on the state q1.

When we see input character zero on state q1, we stay in the same state.

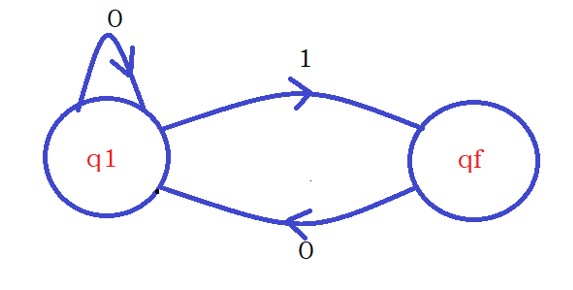
The fourth step is to know we are on state q1, and the input character is ‘1’. So we move to state qf.

Fifth step: Know we are in state qf. the input we see is ‘1’.

We stay in the same state if we see the input character ‘1’ on the state qf.

Assume if the input character is the last character, we should end up on state qf. so we stay on state qf.

The below diagram shows the final logic.

For the understanding purpose, we are showing an example to convert the diagram to a program.

With this conversion, the reader gets an intuition why we design logic using the above diagram.

Conversion:

q1()
{
     Read the next character
     if (no input character)
           printf("string not accepted")
     else if(input=='1')
           return qf() # we calling the function qf
     else if(input=='0')
           return q1()
}
Similarly, write code for function qf

The above function on reading the input character. If no input character, we end up on state q1.

So we displayed the message not accepted.

Similarly, the reader can try to write function for state qf.

In The function qf, if the input is not present, we display the message string accepted because qf is the final state.