DFA Example 2
For Complete YouTube Video: Click Here
In this class, We discuss DFA example 2.
The reader should have prior knowledge of DFA example 1 and DFA example on the dead state. Click here.
Please follow the course from the beginning for a better understanding of the Theory of computation.
We are moving step by step according to the complexity of the logic.
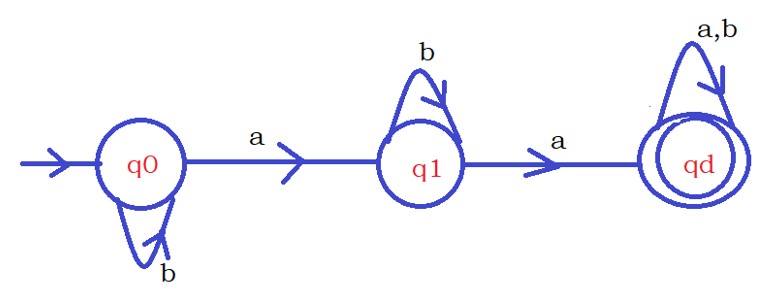
First Question: Design DFA that accepts all the strings with exactly one a.
The input symbols are Σ {a,b}.
From the given question, we need to find the string with exactly one a.
So we take a step whenever we find an input character a.
On the state q0, if we find the input character a, we move to state q1.
If we find more than one input character a. we need to stop checking our logic, so we move to a dead state.
On the state q1, if we find the input character a., we move to the dead state.
We are not bothered about input character b., so we stay in the same state.
The below diagram shows the complete DFA.
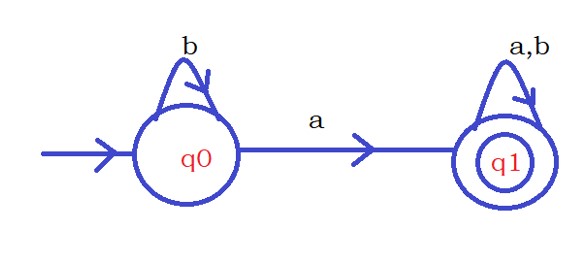
Second Question: Construct DFA which accepts strings with atleast one a.
The input symbols are Σ {a,b}.
We need to find atleast one a from the input string. So whenever we encounter the input character a, we take a step.
On state q0, if we encounter the input character a, we move to state q1.
The state q1 is considered the final state. Because after finding one a, our logic is completed. No need to check the logic further.
On the state q1, if we find the symbol 0 or 1. we stay on the state q1.