DFA Practice Examples

For Complete YouTube Video: Click Here

In this class, We do DFA Practice Examples.

The reader should have prior knowledge of DFA examples from previous classes.

Here, we do practice examples. the concept related to these examples is discussed in previous examples.

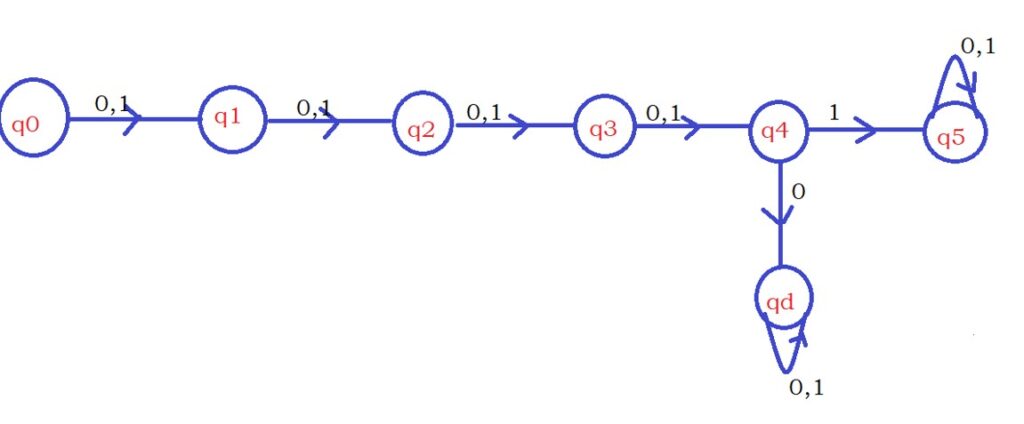
First Example: Design DFA for the given expression.

Expression: a(ab)*aa.

The input symbols are Σ {a,b}

We discuss the expressions in our later classes.

For constructing the DFA, let’s understand the expression.

The above expression will generate strings start with a and end with aa.

The middle expression (ab)* will generate ‘ab’ any number of times.

The string ‘ab’ can be occurred zero times, one time, two times. so on

The sample strings generated are given below.

‘aaa’ this string has ‘a’ at the beginning and ‘aa’ at the end, in between zero times ab.

‘aabaa’ This string has ‘a’ at the beginning and aa at the end, in between one-time ab.

aababaa: This string has ‘a’ at the beginning and aa at the end, in between two times ab.

We have to construct DFA that accepts the strings generated by the above expression.

The first character should be a. So on state q0, when we encounter the input character a, we move to state q1.

On the state q0, if we see the input character one, we move to a dead state because there is no need to check the remaining logic.

ababab we have to check the combination repeatedly. For this, we use the counting logic from previous examples. Click here.

On state q1, if we see the input character a, we move to state q2.

On the state q2, if we see the input character b, we move to state q1. We are counting ababab. So on.

On the state q2, if we encounter the symbol a, we move to state q3 because we have seen the last two characters as a.

Remaining all possibilities, we move to a dead state.

Second Question: Design DFA that accepts strings contain the number of zeros multiples of 5 and one’s multiples of 3.

The input symbols are Σ {0,1}

The below diagram shows the DFA that accepts strings contains zeros multiples of 3.

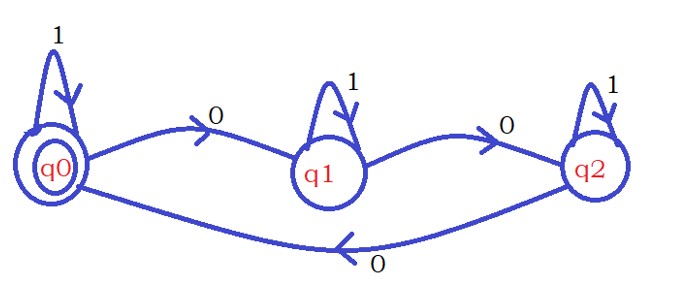
The logic for the above example is explained in the previous classes. Click here.

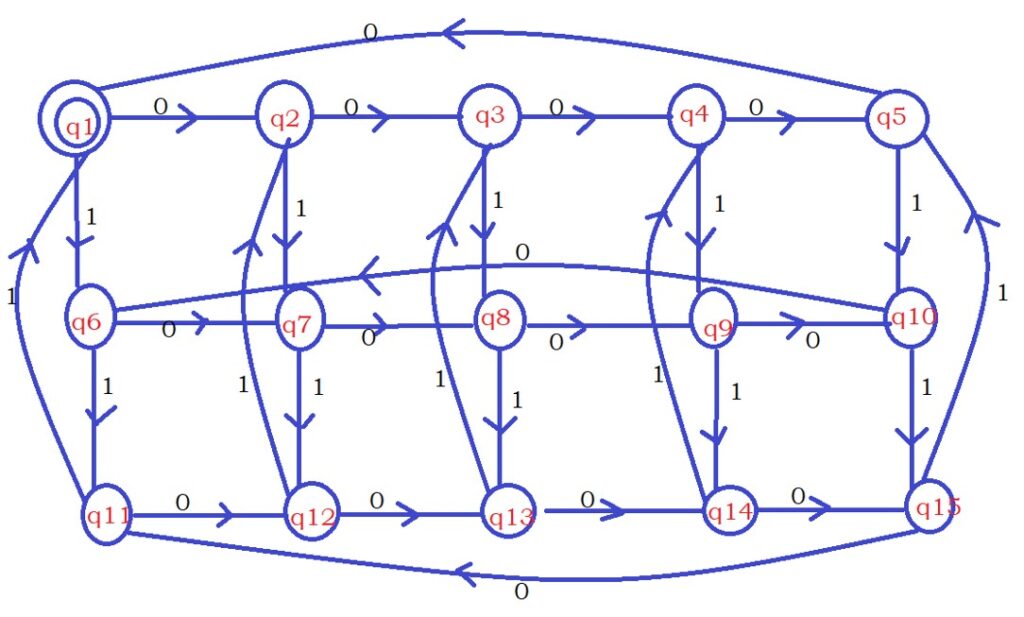
In our example, we need to apply conditions on both zeros and ones.

We follow the layered approach discussed in counting examples.

The below diagram shows the Complete DFA.

Third Example: Design DFA that accepts strings containing fifth symbol 1.

The input symbols are Σ {0,1}

The first four characters should be any character.

In our logic, we move to the next state for the first four characters.

The fifth character should be 1.

On the state q4, if we see the input character one, we move to state q5.

We consider state q5 as the final state.

On the state q4, if we see the input character 0, we move to the dead state.

The below diagram shows the Complete DFA.