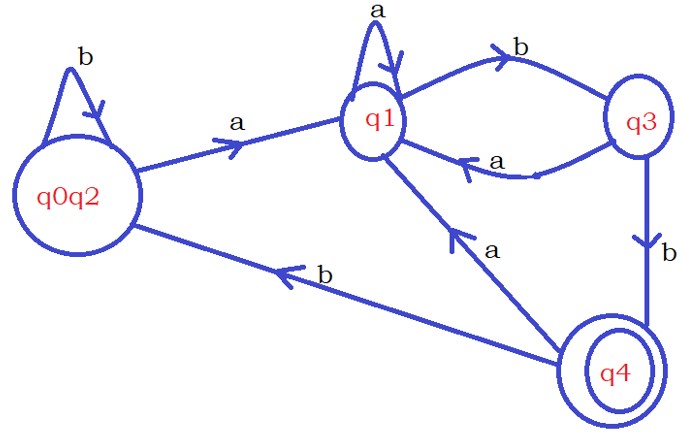
Minimization of DFA Example

For Complete YouTube Video: Click Here

In this class, We discuss Minimization of DFA Example.

The reader should have prior knowledge of DFA examples. Click Here

Why is the minimization of DFA needed?

Suppose we have chosen two persons. And ask them to construct DFA.

One person may construct one way. And the other may follow another logic.

One of the people has written the logic in a lengthy manner.

We get the shortest possible DFA With the help of the minimization of DFA.

To understand the minimization of DFA., Take the below DFA.

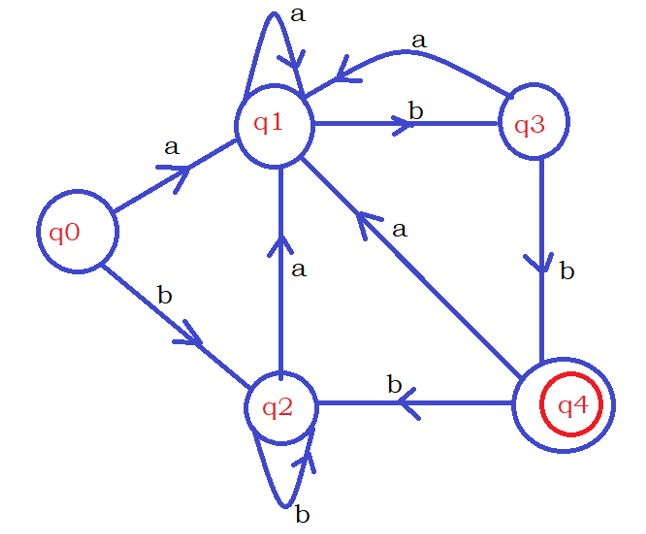
First step: Remove the states that are not reachable from the initial state.

The states that are not reachable are useless.

The above DFA does not contain any unreachable states.

The initial state is q0, and we can move to any state from the initial state.

Second Step:

Follow the below procedure.

First, we should Separate final and nonfinal states.

In our DFA {q0,q1,q2,q3} are non final states and {q4} is the final state.

we have given the set of nonfinal states as Q1. and the set of final states as Q2.

Now take the transition table of DFA and find the transitions moving to set Q1 and Q2.

The below table shows the complete list.

On the state q0, if we see the input character 0, we move to state q1.

The state q1 is in the set Q1.

The above table fourth column shows the complete data of transitions.

The state q0 is moving to set Q1 and Q1.

Similarly, state q1 is moving to set Q1 and Q1.

Take a look at the fourth column. We did not mention the sets for state q4.

Because in the set Q2, we have only one state q4.

So, no need to divide the set Q2.

In the above table, look at the fourth column where the states q0, q1, and q2 are moving to the same set.

The state q3 is moving to different sets.

So we divide q0, q1, and q2 as one set and q3 as another set, and we have q4 in a set.

Again rename the set as Q1, Q2, and Q3.

The set Q1 contains state q0, q1, and q2.

The set Q2 contains state q3.

The set Q3 contains state q4.

Point to remember: The set Q2 and Q3 have single states. No need to divide.

Try to divide set Q1.

The fifth column shows the transition movement to sets.

The state q0 and q2 are moving to the same set Q1 and Q1.

The state q1 is moving to different sets.

Divide the state q2 to another set. and rename the groups.

The set Q1 contains states q0 and q2.

The set Q2 contains states q1.

The set Q3 contains state q3.

The set Q4 contains state q4.

Again repeat the process.

The sixth column shows the output.

The states q0 and q2 are moving to the same sets.

So we stopped the process here because no more division occurred.

We combine states q0 and q2 as one state because both are moving to the same sets.

The below-given diagram shows the final minimized DFA.