Symbols Alphabet String and Language in TOC
For Complete YouTube Video: Click Here
In this class, We discuss Symbols Alphabet String and Language in TOC.
The reader should have prior knowledge of finite automata. Click Here.
The concepts to understand this class are discussed in our previous classes.
Symbol: A symbol is a single object, an abstract entity that has no meaning by itself.
Example: A, a, π, Θ etc
Alphabet: An alphabet is a finite non-empty set of symbols.
The alphabet is represented using Σ.
Example: Σ = {a,b}.
We used the alphabet in our finite automata examples.
The above alphabet contains the symbols a,b.
The finite automata are defined on the given alphabet.
If the alphabet changes, we need to change the finite automata.
String: A finite sequence of symbols chosen from some alphabet.
Example: Σ = {a,b}.
The example strings are aa, bb, aba, bab, soon.
The input string taken from the alphabet is given as input to the finite automata.
We can generate an infinite number of strings from the given alphabet.
Point to understand: The finite automata will accept a few strings from the strings generated from the alphabet.
Null string: No symbol in the string is considered as an empty string.
The null string is represented using the symbols ε, λ, Λ.
Language: A language is a set of strings taken from a given alphabet.
Using an alphabet, we can generate an infinite number of strings.
But in a language, we consider a set of strings generated from the alphabet.
Example: Take the alphabet Σ = {a,b}.
Language L = set of strings having a length less than or equal to 2.
L= {ε,a,b,aa,ab,ba,bb}
Language of a machine: is a language defined by a machine that accepts a set of strings.
The language of a machine is represented as L(M).
Whatever strings are accepted by the machine, we call it the language of a machine.
Example: Set of strings having last two characters aa. over the alphabet Σ = {a,b}.
The below DFA shows the finite automata accepting strings end with aa.
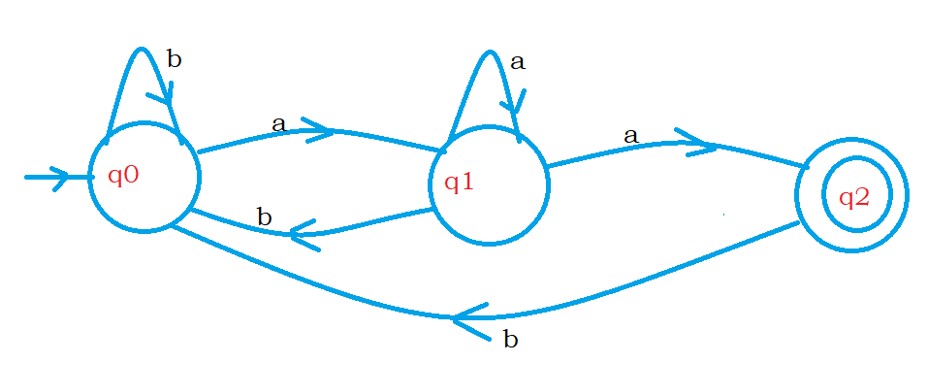
Language L = {aa, baa, babaa, abaa, . . . }
