Deterministic Push Down Automata DPDA
In this class, We discuss Deterministic Push Down Automata DPDA.
For Complete YouTube Video: Click Here
The reader should have a prior understanding of push-down automata. Click Here.
Deterministic Push-Down Automata: A PDA is said to be deterministic if all the derivations in the design have to give only a single move.
The below diagram shows an example for Nondeterministic push-down automata.
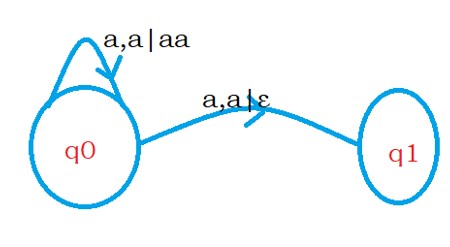
On the state q0, if the input symbol is a and the stack top symbol is a, we are moving to two states.
We do some practice examples to write deterministic push-down automata.
Example 1:
Take the language L = {a^nb^2n where n > 0}
The strings in the language are L = {abb, aabbbb, . . . }
The language has a’s followed by b’s.
If we have a single a, we have two b’s. It means multiples of 2.
The logic is simple.
Whenever we see an input symbol ‘a’, we push it onto the stack.
We need to pop the stack symbol a for every second occurrence of b.
The below diagram shows the DPDA for the language L.
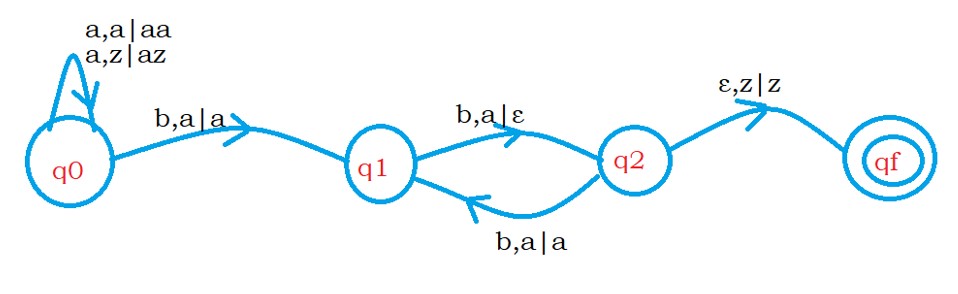
On the state q0, if the input symbol is a and the stack top is z, or a. we push onto the stack.
On the state q0, if we see the input symbol b, we are moving to state q1 and doing no operation.
We have seen the first input symbol b. to change the logic. We move to state q1.
On state q1, if we see the input symbol b, we pop the element from the stack because we have seen the second b.
We move to state q2. and loop on to state q1 for every second occurrence of b.
On the state q2, if the input symbol is epsilon, move to the final state.
Example 2:
Take the language L1 = {wcw^R where w = (0+1)*}
The input alphabet Σ = {0,1,c}.
w^R shows the reverse of the w.
The strings in the language are L1 = {011c110, 001c100, . . . }
The reverse of 011 is 110. After the symbol c, we need to have the reverse of w.
The logic is simple. whatever we find before the symbol c we need to push onto the stack
After the symbol c, the first input should match the stack top. Because we need reverse of w.
After the symbol c, if the input symbol and stack top are the same, we do the pop operation.
The language L1 will accept single c also. Because w can take epsilon.
The below diagram shows the DPDA for the language L1.
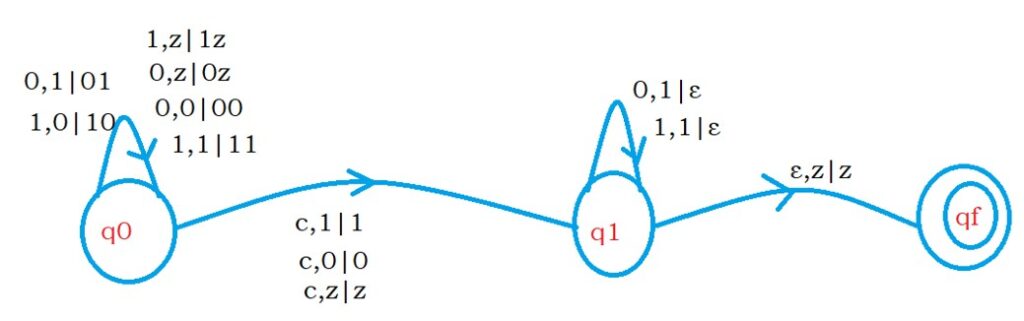
On the state q0, whatever we see, we need to push on to the stack.
On the state q0. If the input is c, move to state q1. Because from now we need to check for reverse
on the state q1 if the input symbol and the stack symbol are the same pop the element.
On the state q1, if the input is epsilon and the stack top is z, we move to the final state.
