Constructing Turing Machine Theory of Computation
In this class, we discuss Constructing Turing Machine Theory of Computation.
For Complete YouTube Video: Click Here
The reader should have prior knowledge of the Turing Machine. Click Here.
Take a language L = { strings containing palindrome} over the alphabet {0, 1}.
The below example is the even palindrome string.
Example: 001100
The below example is the odd palindrome.
Example: 10101
The turing machine should accept both odd and even palindromes.
First, we understand how to construct a turing machine with a few examples.
The turing machine starts from the beginning of the input.
The below diagram shows the input 001100 in the tape memory.
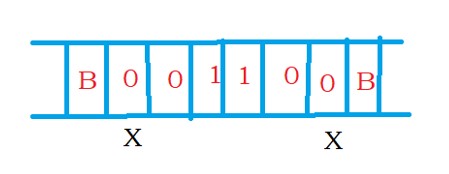
The logic goes as explained below.
The first input symbol is zero, and we replace zero with the tape symbol ‘x’.
We replace zero with the tape symbol ‘x’ because it indicates one zero found in the input.
We move to the right side after converting zero to ‘x’.
In palindrome, if the first symbol is zero. The last symbol should be zero.
We check the first symbol and mark it as ‘x’. Now we have to move to the last symbol.
Suppose the last symbol is zero. We mark it as ‘x’.
How to identify the last input symbol?
Move right until we find a blank symbol.
Whenever we find a blank symbol, we move left. So we stop at the last input symbol.
We converted the first zero to ‘x’. And the last zero to ‘x’.
The process we made above should be repeated for all input symbols.
We are at the last input symbol, so move to the second input symbol.
We move left to find the symbol ‘x’ or ‘y’ on the tape.
Whenever we find the symbol ‘x’ or ‘y’, we move right to stay on the second input symbol.
We repeat the above process for all the input symbols.
The below example shows an odd palindrome.
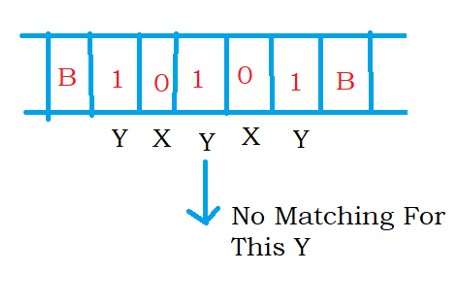
Example: 10101
We convert the first input symbol to ‘y’ and the last symbol to ‘y’.
Similarly, we convert the second input symbol to ‘x’ and the last before symbol to ‘x’.
We find the third input symbol as 1. the third symbol converted to y.
There is no matching input symbol for the third input symbol because it is an odd palindrome.
Still, we have to accept the input because of the odd palindrome.
After finding the third input symbol, we convert it to ‘y’ and move right.
The right side will have ‘x’ or ‘y’ because there is no matching input symbol.
Now, we go and construct a turing machine for palindrome.
The below diagram shows the turing machine for accepting zero’s in palindrome.
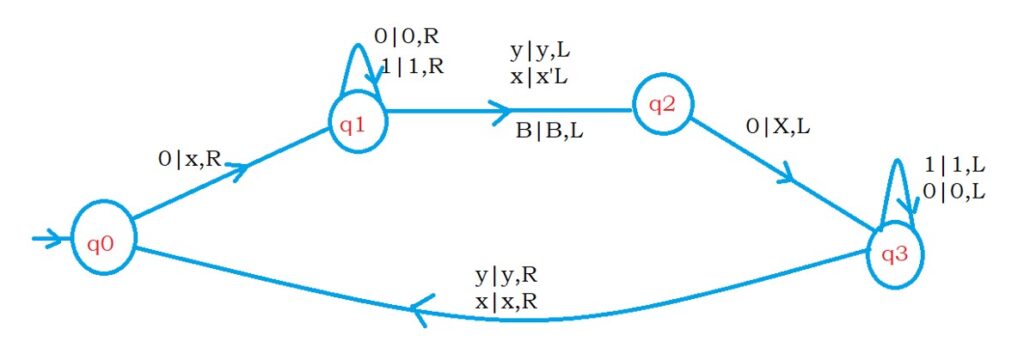
In the end, we extend the same diagram for accepting ones in palindrome.
Example input String: 001100
We start from state q0.
On state q0, if the input is zero. Convert to x and move right. We move to state q1.
The state q1 is used to move to the right of the input.
On q1, if we see input symbol 0 or 1, keep them as 0 or 1. and move right.
We stay on state q1.
On state q1, if the input is blank, keep it blank and move left.
We move to state q2.
The first time we may see the blank symbol, and the next time we may see the symbol ‘x’ or ‘y’.
On state q1, if we see the input symbol ‘x’ or ‘y’. Keep them the same and move left.
We move to state q2.
On the state q2, if the input symbol is zero, convert to ‘x’ and move left.
We move to state q3.
We use the state q3 to move to the left side.
On state q3, if the input is 0 or 1, keep them the same and move left.
On the state q3, if the input is ‘x’ or ‘y’, we move right.
We move to state q0.
After converting first zero and last zero, we moved to state q0.
Repeat the process.
The below diagram shows the extra conditions for stopping the turing machine.
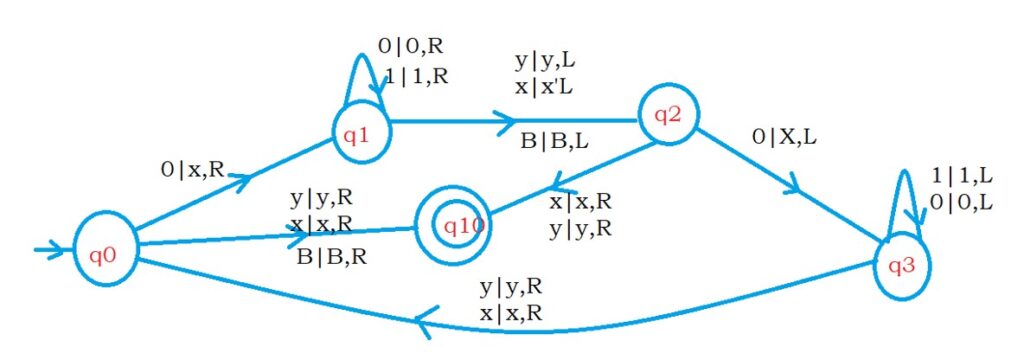
On state q0, if we see the input symbol ‘x’, ‘y’, or ‘B’, keep them the same and move to the right.
We move to state q10.
The state q10 is the halt state, and the transition mentioned above accepts even palindromes.
The below transition is to accept odd palindromes.
On state q2, if the input is ‘x’ or ‘y’, move right.
We move to state q10.
The below diagram shows the complete turing machine for accepting palindromes.
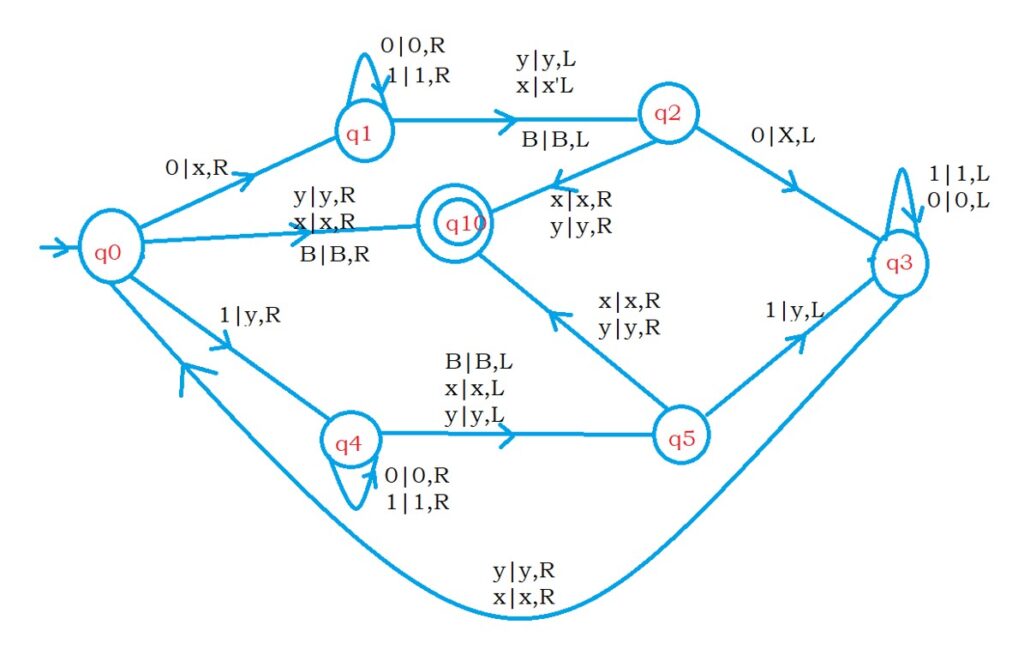
We added q4 and q5 states to accept 1 in the input string.
On state q0, if the input is one, we move to q4 state.
The state q4 is similar to q1. We used to move till right.
We use the state q5 similar to state q2.
