Turing Machine as Subtractor
In this class, We discuss Turing Machine as Subtractor.
For Complete YouTube Video: Click Here
The reader should have prior knowledge of the Turing machine as an adder. Click Here.
First, We understand proper subtraction.
f(m, n) = m – n if m is greater than n else zero.
We do proper subtraction in unary numbers.
The discussion of unary numbers is made in the Turing machine as an adder class.
Example:
m = 5 is represented as five zeros.
n = 2 is represented as two zeros in the unary number system.
The below diagram shows the representation of m and n in tape.
We use zero to separate the values m and n.
Logic:
We need to identify logic for three conditions.
1) m > n
2) m = n
3) m < n
We start at the starting of the input string.
5 -2 = 3

On executing the Turing machine, the tape has to be filled with three zeros.
First, we convert the first one into blank and move right.
We move right till we find a blank symbol and move left.
The last one in the number n is converted blank.
Now we need to move left till we find a blank and move right.
We come to stay on the second one in the input number m.
Convert the second one into blank and move right till we find blank.
Now convert the second one from last in number n.
We move left and convert the third one in the number m.
We did not find the third one on the number n.
So we find zero on when we move to the number n.
The number m is big. because we found an extra one in the number m.
m = n
The below diagram shows the example input on the tape with m = 2 and n =2.

We convert the first one in number m and move to last.
We convert the last one in number n and move left.
After converting two ones in number m and number n, the third one is not found on number m. we find zero.
Whenever we find zero, the number m is completed.
If both the numbers are equal, we output value zero.
The value zero in unary numbers is all blanks. So we convert the zero to blank.
m < n

If the number m is less, we need to output zero.
The logic is similar to m = n.
Whenever the ones in the number m are over, we need to convert the remaining ones in number n to blanks.
The below diagram shows the Turing machine for subtraction.
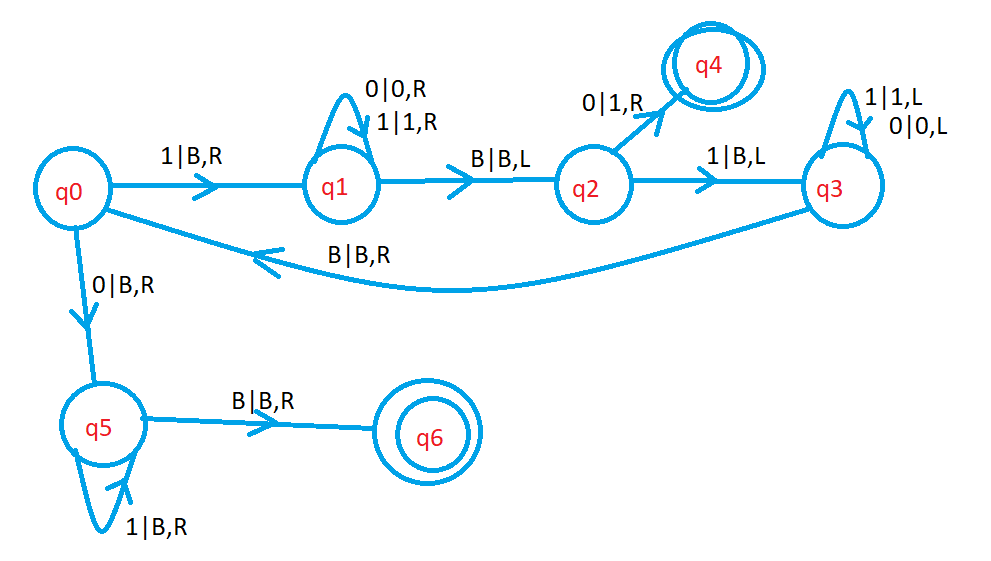
We start from state q0.
On the state q0, if the input is one, we convert to blank and move right.
The state q1 is used to move right till we find a blank.
On the state q1, if the input symbol is 0 or 1, we move right.
On state q2, if we see input symbol one, we convert one to blank.
The condition m > n is mentioned on state q2 with input zero.
The state q3 is used to move left till we find a blank.
On the state q0, if we see input zero, we write the condition m <= n.
We convert the zero and ones to blanks.
