Median Frequency Distribution Examples
In this class, We discuss Median Frequency Distribution Examples.
For Complete YouTube Video: Click Here
The reader should have prior knowledge of finding the median for frequency distribution. Click Here.
Example 1:
Three thousand employees work in a factory.
5% of employees work less than 3 hours.
Five hundred eighty employees work 3.01 to 4.50 hours a day.
30% of employees work for 4.51 to 6.00 hours a day.
Five hundred employees work 6.01 to 7.50 hours a day.
20% of employees work 7.51 to 9.00 hours a day.
The rest of the employees work above 9.01 hours a day.
The question shows the distribution is continuous.
The below table shows the data of continuous distribution.
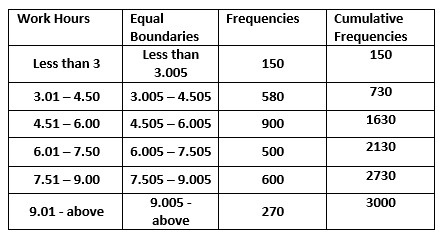
In continuous distribution, we need to equal the boundaries.
We take the average of boundaries and equate them.
The second column in the table shows the updated continuous data values.
First, we find the cumulative frequency and substitute the median class values in the equation.
Median = L + (h/f)((N/2)-c)
N/2 = 1500
The median class is 4.505 – 6.05.
c = 730.
h = 1.500
f = 900
Median = 4.505 + (1.5/900)(1500 – 730).
Median = 5.788
Example 2:
Given N = 229
Median m = 46.
The below table shows the data distribution and cumulative frequency.
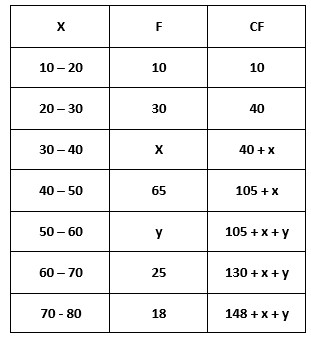
we need to identify the x and y values?
Solution:
From the cumulative frequency we have 148 + x + y = 229.
x + y = 89
Median value is provided in the question m = 46.
The median class is 40 -50.
c = 40 + x.
Substitute in the equation L + (h/f)((N/2)-c).
46 = 40 + (10/65)(114.5 – (40+x))
x = 35.53.
x = 36
Substitute x in x + y = 81.
y = 81 – 35.53.
y = 45.5
y = 46
