Geometric Mean Given Frequencies
In this class, We discuss Geometric Mean Given Frequencies.
For Complete YouTube Video: Click Here
The reader should have prior knowledge of geometric mean. Click Here.
Example 1:
The below table shows the data distribution.
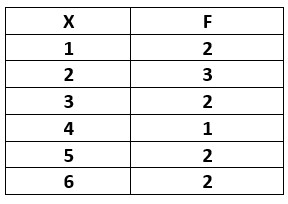
GM = ((x1)^f1 * (x2)^f2 * . . . (xn)^fn)^(1/N)
N = 1 to nΣfi
GM = (1^2 * 2^3 * 3^2 * 4^1 * 5^2 * 6^2)
GM = 2.826
Example 2:
The geometric mean of ten observations was 16.2.
One data value was recorded as 12.9 instead of 21.9.
Calculate the correct geometric mean.
GM = (x1, x2, . . . ,xn)^1/n
x1 = 12.9
GM = 16.2
x1′ = 21.9
GM’ = ((x1’/x1), x1, x2, . . . x10)^1/n
GM’ = (x1’/x1)^1/10 (x1, x2, . . . x10)^1/10
GM’ = (21.9/12.9)^1/10 * (16.2)
GM’ = 17.08
