Standard Deviation Examples
In this class, We discuss Standard Deviation Examples.
For Complete YouTube Video: Click Here
The reader should have prior knowledge of standard deviation. Click Here.
Example 1:
The below table shows the data and values needed to find the standard deviation.
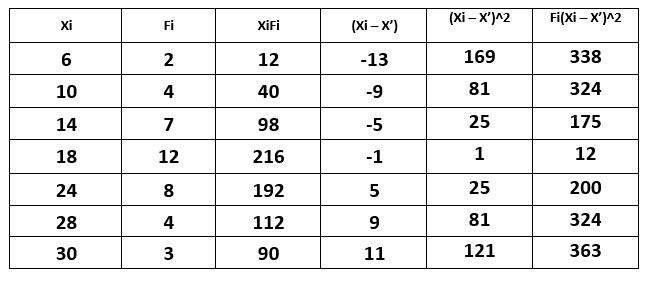
Column Xi shows the data values.
The column Fi shows the frequency values.
First, we need to find the mean value given frequencies.
We find XiFi and use the values to find the arithmetic mean.
Arithmetic mean = X’ = ΣXiFi/ΣFi = 760/40 = 19
N = ΣFi = 40
we find the Fi(Xi – X’)^2 for standard deviation.
Standard Deviation = σ = √1/N Σ fi (Xi – X’)^2
σ^2 = 1736/40
σ = √43.4 = 6.58
Example 2:
X1′, σ1be mean and standard deviation of size n1
X2′, σ2 be mean and standard deviation of size n2.
Find the mean and standard deviation of the combined sample n1 + n2?
Solution:
X’ = combined sample mean = (n1x1′ + n2x2′)/(n1 + n2)
The equation of combined arithmetic mean explained here.
combined standard deviation = σ = √(n1σ1^2 + n2σ2^2 + n1D1^2 + n2D2^2)/(n1+n2)
D1 = X1′ – X’
D2 = X2′ – X’
Example:
The below table shows the mean and standard deviation of three data samples.
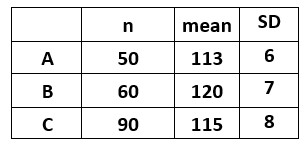
Mean = X’ = (n1x1′ + n2x2′ + n3X3′)/(n1 + n2+ n3)
Substituting the values we get X’ = (50 * 113 + 60 * 120 + 90 * 115)/ (50 + 60 + 90)
X’ = 116
D1 = X1′ – X’ = 113 – 116 = -3
D2 = X2′ – X’ = 120 – 114 = 6
D3 = X3′ – X’ = 115 – 116 = -1
combined standard deviation = σ = √(n1σ1^2 + n2σ2^2 + n3σ3^2 + n1D1^2 + n2D2^2 + n3D3^2)/(n1+n2 + n3)
σ = 7.746
