Omega Notation

For Complete YouTube Video: Click Here

In this class, we will try to understand What is Omega Notation.

The definition of Asymptotic notation, Big O Notation, was explained clearly in our previous class.

Omega Notation

The definition of the Omega Notation is as shown below.

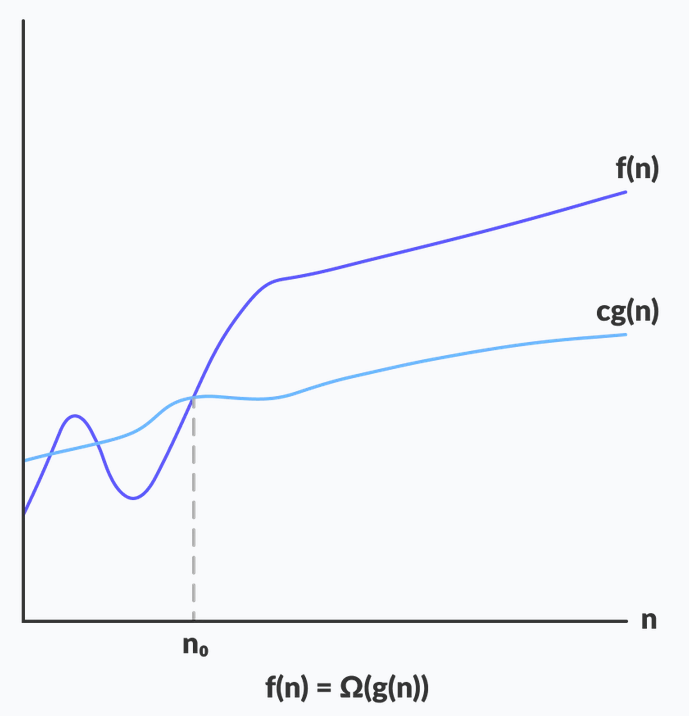
The function f(n) = Ω(g(n)) if and only if there exists positive constants c and n0 such that f(n) >= c * g(n) for all n, where n >= n0.

The above definition states that function f(n) can be expressed as Ω(g(n)) (Omega of g of n) when f(n) is greater than or equal to some constant c * g(n) for all the values of n where n is greater than or equal to n0.

This definition is proven for any function f(n). In our course, we consider f(n) as the time complexities of the algorithms.

To understand the definition better, we will consider the example shown below.

For example, the time complexity of an algorithm is 3n + 2.

This 3n + 2 can be expressed in Omega notation if we can prove that 3n + 2 is greater than or equal to c*g(n) for all the values of n where n >= n0.

Consider 3n + 2 >= 3n for all the values of n >= 1 (n0 = 1).

The above expression is true for all the values of n >= 1.

If n = 1 then 3n + 2 >= 3n is true.

If n = 2 then 3n + 2 >= 3n is true.

If n = 3 then 3n + 2 >= 4n is true.

Simillarly, for n = 10, 3n + 2 >= 4n is true.

In such cases, we can say that 3n + 2 = Ω(g(n)).

How does the Omega notation describe an algorithm?

We will get the lower bound for the function with the Omega.

For all the values of n >= 1, 3n + 2 will always cross 3n.

The image below shows the Omega notation on a graph.

For a clearer and better understanding, click on the top and learn for free.