Understanding Order of Growth of an Algorithm
For Complete YouTube Video: Click Here
In this class, we will try Understanding Order of Growth of an Algorithm.
We have already discussed the concept of time complexity in our previous classes.
Table of Contents
Understanding Order of Growth of an Algorithm
To understand the concept of Order of Growth of an algorithm, we will consider the following time complexities of algorithms.
The time complexity of Algorithm A: 100n + 1
The time complexity of Algorithm B: n2 + n + 1
As shown below, let’s try to analyze the number of steps these algorithms execute as the input size increases.
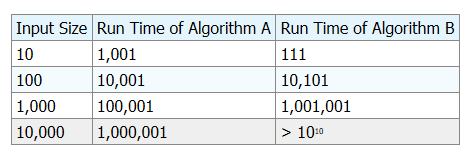
At the input size of 10, Algorithm A will execute more steps than algorithm B.
At the input size of 100, both algorithms will execute almost equivalent steps.
At the input size of 1000, the number of steps executed by algorithm B is more compared to algorithm A.
The important point to understand is as the input size increases, the significance of the lower-order tems and the coefficients of higher-order tems is negligible.
The number of steps executed by the algorithm or order of growth of an algorithm is dependent on the higher-order term.
Definition of Order of Growth
Order of growth is a set of functions whose asymptotic growth behavior is considered equivalent.
From the above definition, consider the following time complexities of the algorithms.
{n, 2n, 100n, n + 1}
From all the above set of time complexities, all algorithms’ growth behavior is equivalent to n.
