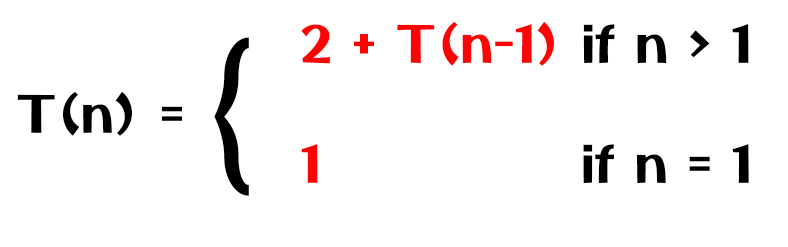Recurrence Relation of Recursive Algorithms

For Complete YouTube Video: Click Here

This class will try to understand the Recurrence Relation of Recursive Algorithms.

We have already discussed the concept of recursion in our previous class.

Table of Contents

In the Discrete Mathematics course, we have clearly explained the recurrence relation concepts.

This class shows how the recurrence relations are used in algorithms.

We have seen how to find the efficiency of iterative algorithms in our previous classes.

We must first find the recurrence equations to find the efficiency of recursive algorithms.

By solving those recursive equations, we will get the efficiency of recursive algorithms.

To solve the recursive algorithms, we have two methods.

To understand this consider the factorial algorithms shown below.

Any recursive algorithm is divided into two parts.

The base part (if condition part) is used to stop the flow of recursion.

The recursive part (else part) is for the execution of the algorithm.

First, we will find the time taken by the recursive part of the algorithm.

The recursive part will get executed only when the value of n is greater than one.

The equation is T(n) = 2 + T(n-1).

The base will execute only one line of code, the return statement.

The overall equation is shown below.