Merge Sort Working Mechanism

For Complete YouTube Video: Click Here

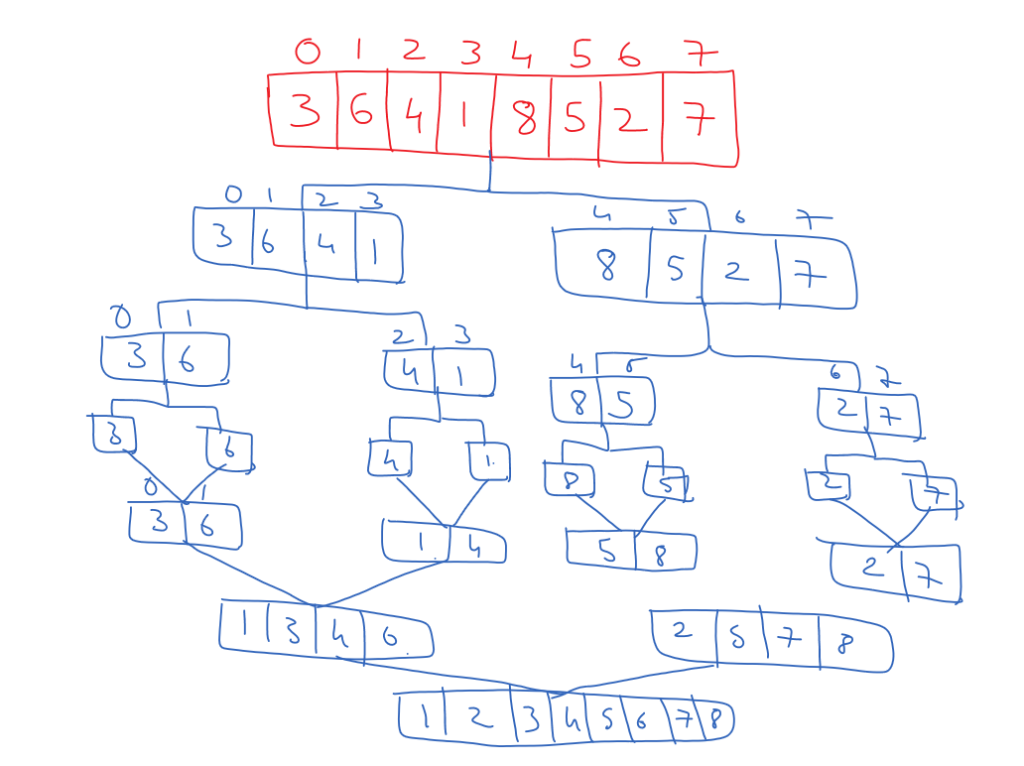
This class will try to understand Merge Sort Working Mechanism.

The understanding of the concepts discussed in our previous class is essential for what we discuss in this class.

The Merge Sort Working Mechanism is based on the “divide and conquer” design technique.

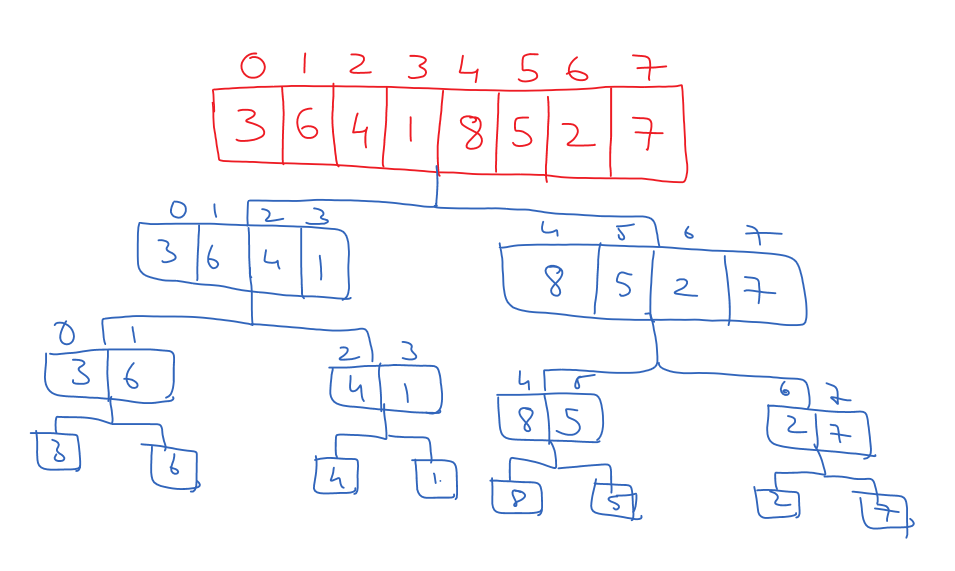
To understand this, we will consider the array of elements shown below.

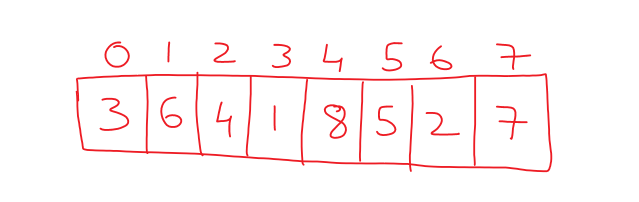
The merge sort will divide this array into two halves to arrange these elements in the sorted order.

The division of the array is done by finding the middle value.

We can get the middle value by using q = floor( (Low + High) / 2).

From the above formula, the low is the small index of the array, and the high is the highest index of the array.

In our case, Low = 0 and High = 7.

Now, q = 3.

The array will be divided into two halves, from index 0 to 3 and from 4 to 7, as shown below.

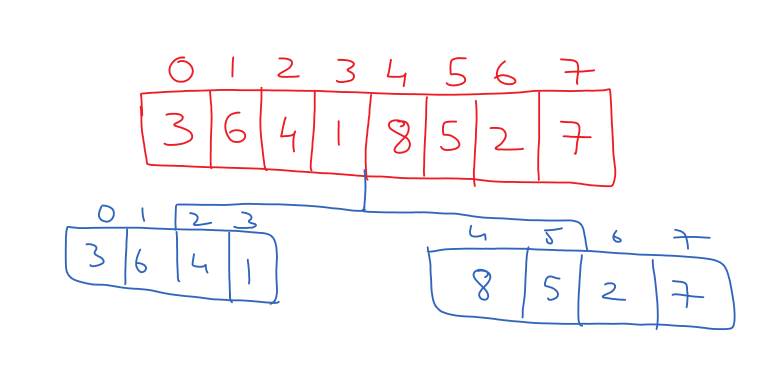
Dividing the array means logically, not physically.

On that part of the array, the sorting is made.

Now the sub-problem from 0 to 3 and 4 to 7 can further be divided into sub-problems.

So, those sub-problems are divided further, as shown below.

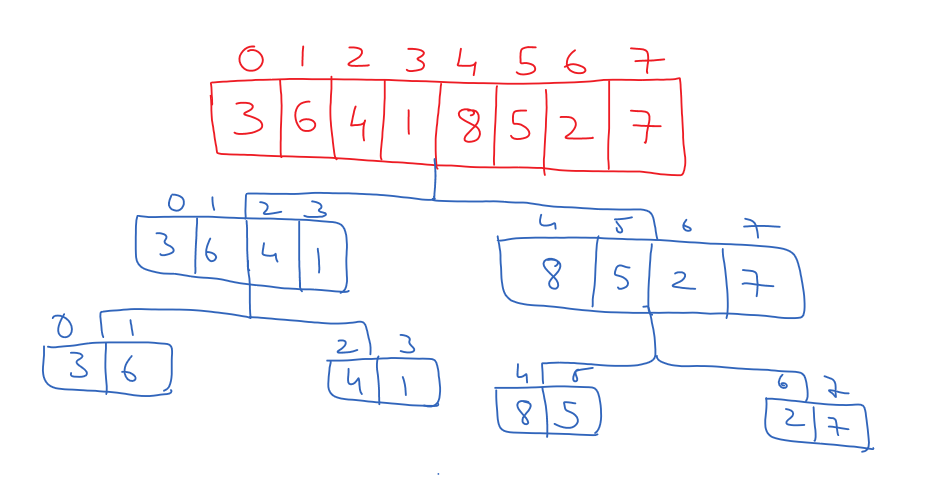
The division will stop if we have only an element in the sub-problem, as shown below.

Now, the conquer is done on the sub-problems.

Conquer means the elements in the sub-problem will get arranged in the sorted order.

Once they get sorted, the elements will get combined.

The final visualization of the merge sort is shown below.