Standardizing Normal Random Variable

In this class, We discuss Standardizing Normal Random Variable.

The reader should have prior knowledge of standard normal distribution. Click Here.

We take an example and understand the concept.

Example:

Take a normal distribution with a mean of ten and a standard deviation of 2.

The below diagram shows the normal distribution.

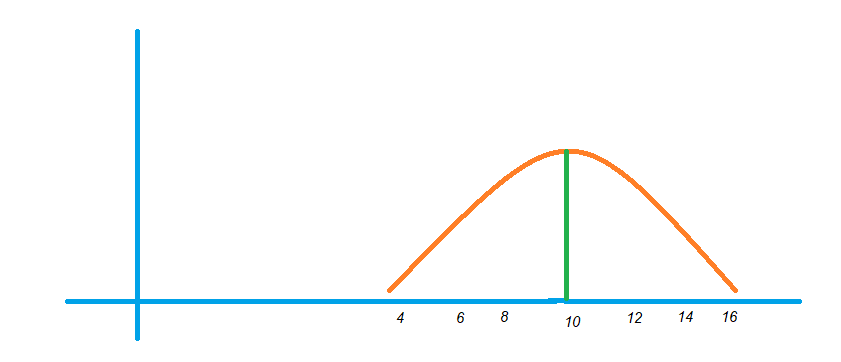
Find the probability value P(8 < X < 12)?

The below equation shows how to find the probability.?

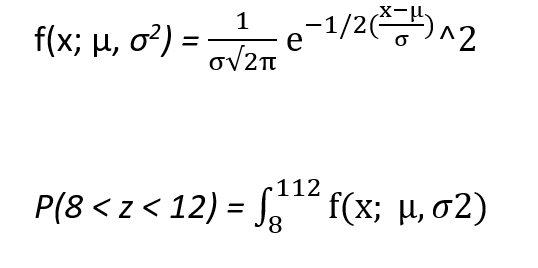
Finding the probability using an integral equation is difficult.

We discussed standard normal distribution and finding probabilities using the table in our previous classes.

We use the same table to find the probabilities of the above normal distribution.

First, we will understand how we find the probability.

In the end, we understand why both are the same.

Standardization:

Standardization is the procedure to convert the normal random variable to a standard normal random variable.

Z = (X – μ)/σ

Z1 = (8 – 10)/2 = -1

Z2 = (12 -10)/2 = 1

Z1 and Z2 are standard normal random variables.

Now, we identify probability using standard normal distribution P(Z1 < X < Z2).

We use a normal table to find probabilities in a standard normal distribution.

The probability from a standard normal distribution is the same as the probability of normal distribution.

Why are they both the same?

The normal distribution random variables are 8 and 12.

The random variables are one standard deviation from the mean on both sides.

The random variables after standardizing are -1 and 1, which are one standard deviation away from the mean.

Both probabilities are the same from property 4. Click here for properties.