Pipes and Cistern Complex Examples

In this class, We discuss Pipes and Cistern Complex Examples.

For Complete YouTube Video: Click Here

The reader should have prior knowledge of pipes and cistern formulae. Click Here.

Example 1:

Two pipes, A and B, can fill a tank in 36 and 45 minutes, respectively.

A water pipe C can empty the pipe in 30 minutes.

First, A and B are open for seven minutes. After 7 minutes, C is opened; how much time will it take to fill the tank?

Solution:

The below diagram shows the graphical intuition for the example.

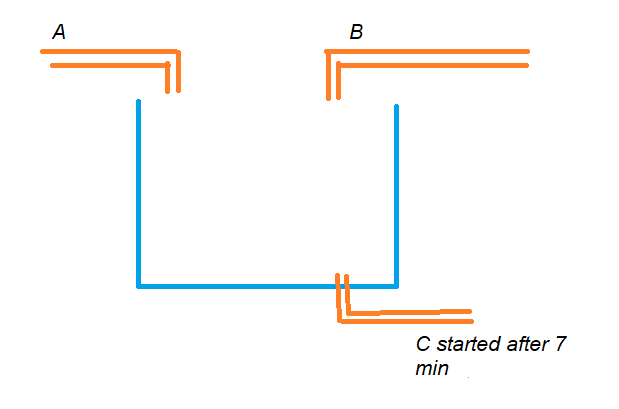
A and B work simultaneously for seven minutes.

Basic formulae identify A and B’s one-minute capacity.

Total capacity is filled in 7 minutes, and the remaining part is considered.

A’s one minute = 1/36

B’s one minute = 1/45

(A + B).’s one minute = (1/36 + 1/45)

(A + B).’s seven-minute = 7(1/36 + 1/45) = 7/20

Remaining part = 1 – 7/20

= 13/20

Net part filled in one minute when A, B, and C are working simultaneously = ( 1/36 + 1/45 – 1/30) = 1/60

1/60 part filled in one minute

13/20 part filled in how many minutes?

= (13/20)/(1/60) = 39 minutes

Total Time = 39 + 7 = 46 minutes.

Example 2:

Two pipes, A and B, can fill a tank in 24 and 32 minutes, respectively.

If both the pipes opened simultaneously, then after how much time should B be closed to fill the tank in 18 minutes?

Solution:

The below diagram shows the graphical intuition of the example.

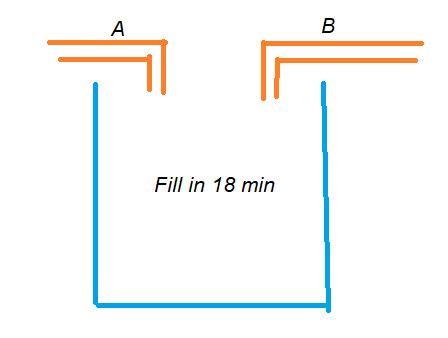
A’s one minute = 1/24

B’s one minute = 1/32

Let B be closed after x minutes.

Part filled by A + B in x minutes + Part filled by A in 18-x minutes = 1

x[1/24 + 1/32] + (18-x) 1/24 = 1

7x/96 + (18 – x)/24 =1

7x + 4(18 – x) = 96

x = 8

Closed after 8 minutes.