Ratio of Speeds Train Problems Formula

In this class, We discuss Ratio of Speeds Train Problems Formula.

For Complete YouTube Video: Click Here

The reader should have prior knowledge of the train problems formula. Click Here.

If two trains are bodies, start simultaneously from points A and B towards each other.

After passing each other, they take b and a second to reach B and A, respectively.

A’s speed: B’s Speed = √b: √a

The below diagram shows the graphical intuition of the example.

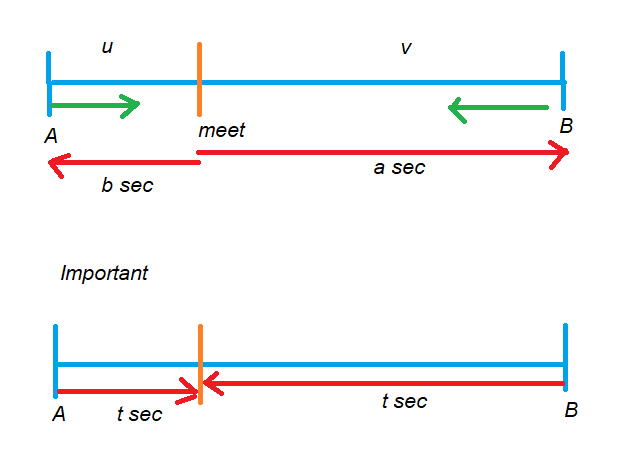
Important: The two trains meet at some point.

The time traveled before the two trains meet t seconds.

The above point helps in solving the formula and helps in solving the bits.

After the two trains met, Train A traveled seconds to reach B.

Train B traveled b seconds to reach A.

Assumption: The speed of the train started at A is ‘u’ m/s.

The speed of the train started at B is v m/s.

The two trains meet at a point. When the two trains met, they covered the distance from A to B.

Distance from A to B is x.

Distance = speed * Time

x = t (u+v) equation 1

x = (t+a)u equation 2

x = (t+b)v equation 3

Equate 1 and 2 equations.

ut + vt = ut + ua

vt = ua

Equate 1 and 3 equations.

ut + vt = vt + vb

ut = vb

t = vb/u

Substituting we get

v(vb/u) = ua

v^2 b = u^2 a

u/v = √b/√a