Relative Speed Train Problems

In this class, We discuss Relative Speed Train Problems.

For Complete YouTube Video: Click Here

The reader should have prior knowledge of the relative speed formula. Click Here.

Example 1:

A train 150 meters long is running at a speed of 68kmph.

At what time will it pass a man who is running at a speed of 8kmph.

The man and the train are moving in the same direction.

Solution:

The below diagram shows the graphical understanding of example 1.

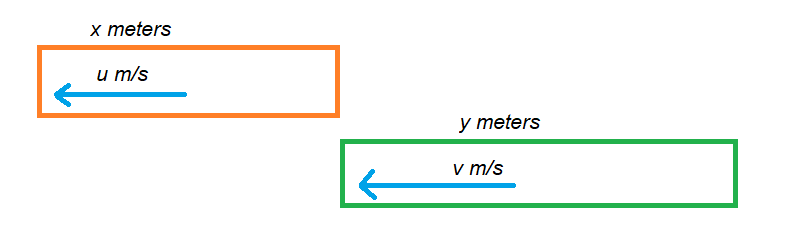
The two trains are moving in the same direction.

From the formulas Time taken for faster train to cross slower train = (x + y)/ (u – v).

In our example, the train is crossing a man.

The man had no length.

Important: Train to cross a man should travel the length of the train.

The below diagram shows the graphical intuition.

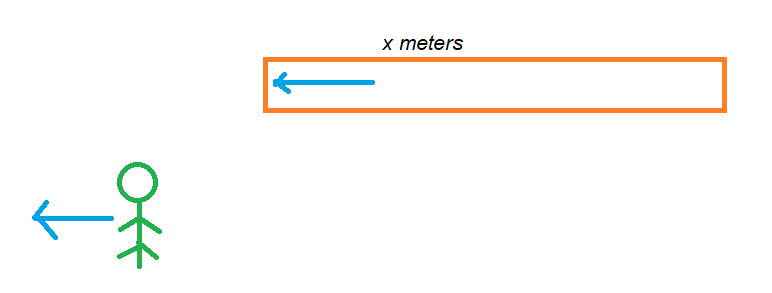
time = x / relative speed.

x = length of the train.

Speed of the train relative to the man = (68 – 8) kmph.

S = 60 * 5/18 m/s = 50/3 m/s

Time taken by the train to cross a man = T = 150/(50/3)

T = 9 seconds.

Example 2:

Two trains, 137 meters and 163 meters in length are running towards each other in parallel lines.

One of the trains at the rate of 42 kmph. And other at the rate of 48 kmph.

At what time will they be clear of each other from the time they meet?

Solution:

The below diagram shows the graphical intuition of the example.

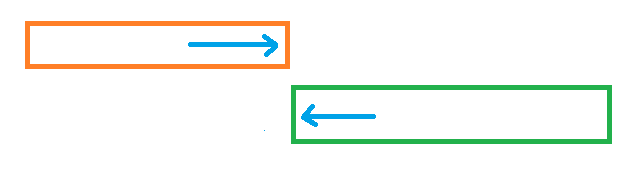
Both trains are moving, so we consider relative speed.

Distance travelled to cross each other = sum of the lengths of the trains.

Relative speed = (42 + 48) kmph

S = 90 kmph = 90 * 5/18 = 25 m/s.

Time = Distance / speed

T = (137 + 163)/ 25

T = 12 seconds.

Example 3:

Two 100 meters and 120 meters long trains are running in the same direction.

The speeds of the trains are 72 kmph and 54 kmph, respectively.

How much time will the first train cross the second?

Solution:

Time = Distance / speed

Distance = 100 + 120 meters = 220 meters.

Speed = Relative speed = (72 – 54) kmph

S = 18 * 5/18 = 5 m/s

T = 220/5 = 44 seconds.