Time and Distance Ratios Examples

In this class, We discuss Time and Distance Ratios Examples.

For Complete YouTube Video: Click Here

The reader should have prior knowledge of the time and distance formula. Click Here.

Example 1:

A certain distance is covered by a bike at a certain speed, and

if the cyclist covers half the distance in double the time.

The ratio of speeds of cyclists to that of a bike?

Solution:

Assume, Distance = D

Bike:

Speed = x

Time = Distance / Speed

t = D/x

Cyclist:

2t = (d/2)/y

Speed of cycle = y

y = d/4t

y : x = (d/4t) : (d/t)

y : x = 1 : 4

Important: when they ask for ratios, we can cancel the distance and time. This point should come to your mind.

Example 2:

Three persons are walking from place A to Place B.

Their speeds are in the ratio of 4 : 3: 5.

The ratio of their times is?

Solution:

From the formulas discussed, the ratio of times is inversely proportional to speeds if the equal distance traveled.

1/4: 1/3: 1/5

60/4: 60/3: 60/5

15: 20: 12

Example 3:

A dog takes four laps for every five laps of the rabbit.

Three laps of the dog are equal to 5 laps of the rabbit.

Find the ratio of speeds?

Solution:

A dog takes four laps for every five laps of the rabbit.

In the above statement, we must understand that the dog takes four laps at a certain time t, and the rabbit takes five laps.

Three laps of the dog = five laps of the rabbit.

From the above statement, we have to understand the size of the leaps is different.

Dog lap is big when compared to rabbit lap.

The below diagram shows the laps.

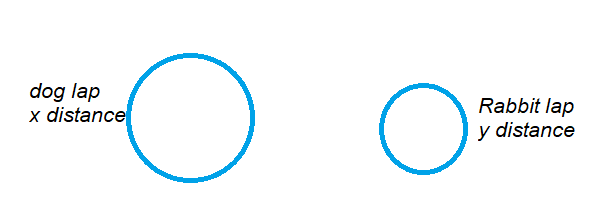
Assume dog lap distance = x

rabbit lap distance = y

3x = 4y

x = 4y/3

The dog takes four laps for every five laps of the rabbit. so 4x = 5y

The ratio of speeds is directly proportional to distance if times are the same.

We made the above statement from the formulas discussed.

s1 : s2 = 4x : 5y

s1 : s2 = 4(4y/3) : 5y

16y/3: 5y

s1 : s2 = 16 : 15