Merge Function in Merge Sort Algorithm

For Complete YouTube Video: Click Here

This class will try to understand Merge Function in Merge Sort Algorithm.

We have discussed the working mechanism of merge sort in our previous class.

The complete algorithm for merge sort is shown below.

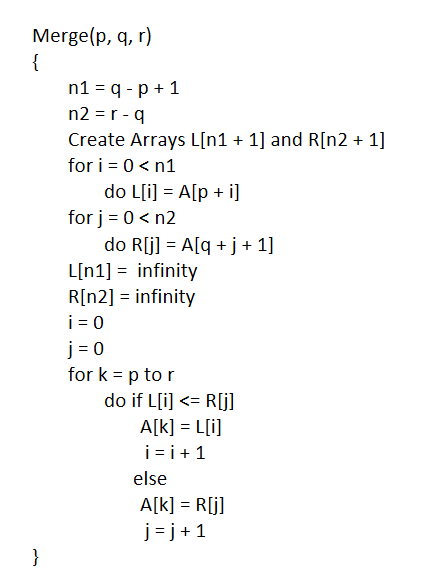
In this class, we will discuss only the merge function.

In the next class, we discuss the complete merge sort.

Merge is part of the merge sort algorithm.

We will consider the array below to understand the merge function.

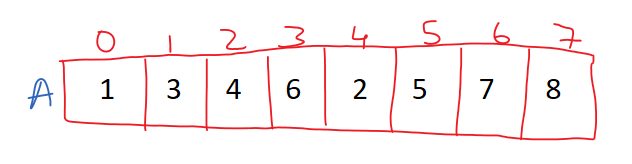
The elements from 0 to 3 and 4 to 7 were already sorted.

Now, we will use the merge function and sort the elements.

The merge function call is merge(0, 3, 7).

The values 0, 3, and 7 are p, q, and r, respectively.

q is the middle value where the array was divided.

The first line of code n1 = q – p + 1 gives the number of elements in the first half of the array.

n1 = 3 – 0 + 1 = 4.

The number of elements in the first half of the array is from 0 to 3 are four.

Similarly, n2 = r – q gives the number of elements in the second half of the array.

n2 = 7 – 3 = 4.

The number of elements in the second half of the array is from 4 to 7 are four.

The third line creates two arrays, L[5] and R[5], as shown below.

The for loop will store the elements in the first half of the array to L[5], as shown below.

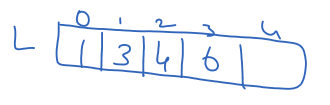
Similarly, the second for loop will store the elements in the remaining half of the array in R[5], as shown below.

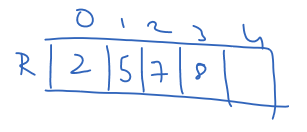
L[n1] = infinity and R[n2] = infinity will store infinity in the place of the last elements, as shown below.

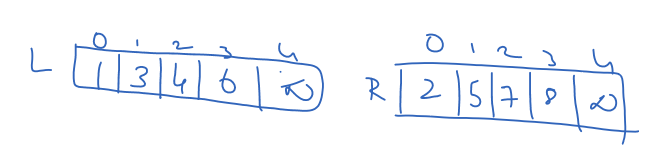
i = 0 and j = 0 were assigned.

Now, the for will iterate from k to p to r.

In our case, the loop will iterate from 0 to 7.

In each iteration L[i] <= R[j] is compared if it is true A[k] = L[i] and i = i + 1 will be made.

Else A[k] = R[j] and j = j + 1 is done.

By the end of for, all the elements will be in sorted order.