Partition Algorithm in Quick Sort

For Complete YouTube Video: Click Here

In this class, we will try understanding Partition Algorithm in Quick Sort.

We have already discussed the Quick Sort working mechanism in our previous classes.

Partition Algorithm in Quick Sort

The partitioning algorithm will rearrange the elements so that the algorithm will bring the pivot element into its position.

After applying the partition algorithm, the elements less than or equal to the pivot element will be arranged on the left-hand side, and the elements greater than or equal to the pivot element will be arranged on the right-hand side.

The image below is the partition algorithm used in the quick sort algorithm.

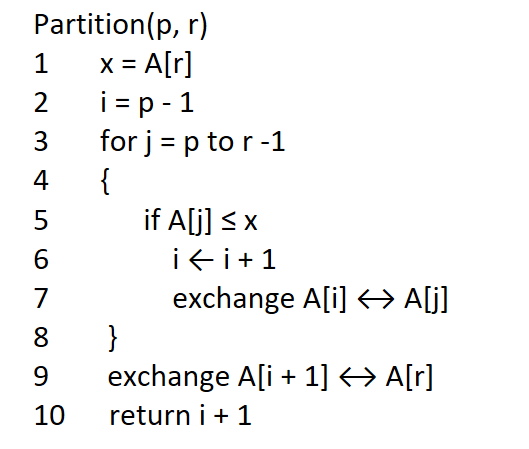
For better understanding, we will consider the array shown below.

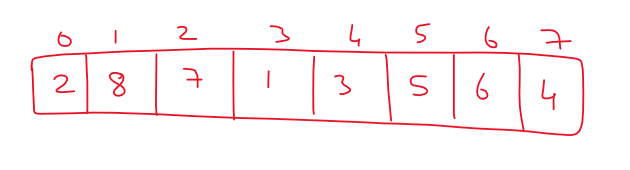
We will start our algorithm with a function called partition(0, 7).

From the above function call the value of p = 0 and r = 7.

In the first line of x = A[r], we consider the pivot element as the last element of the array.

In the second line of code, we will consider the value of i as p-1, i = -1.

Now, the for will come to action.

Understanding for loop is very important.

The for loop will iterate from 0 to 6, representing the size of the array – 1.

Every time we come into the loop, we consider the A[j] <= x in the if statement.

If this happens to be true, we will increment the value of i and swap A[i] and A[j].

The above comparison is all the elements greater than the pivot will get shifted to the right of the final position of the pivot element.

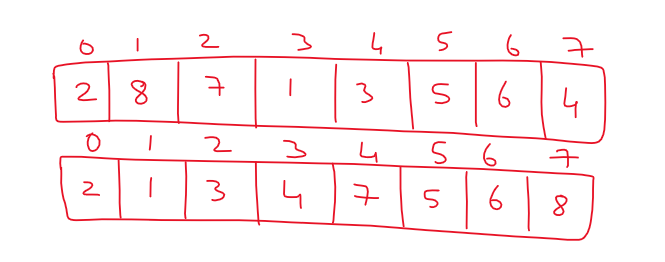
The final array after the rearrangement is shown below.