Quick Sort Algorithm

For Complete YouTube Video: Click Here

In this class, we will try to understand the Quick Sort Algorithm.

We have already discussed the Merge Sort Algorithm in our previous classes.

Understanding merge sort is very important to understand what we discuss in this class because both use the same divide and conquer algorithm design technique.

This class will not discuss the concepts of recursive function calls in detail.

In the merge sort algorithm, we have discussed the concepts of recursive function calls in detail.

Quick Sort Algorithm

The image below is the complete algorithm for the quick sort.

We consider the array shown below for better understanding.

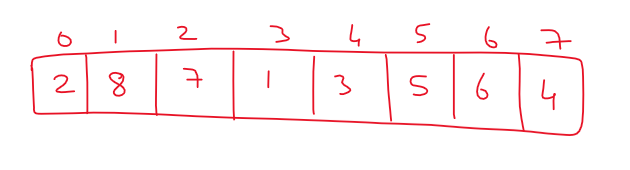
The Quick-Sort(0, 7) function call is made on the above array.

Now the partition function call is made, and after completion of the partition algorithm, the array will be rearranged as shown below.

The partition algorithm will return the index of the pivot element.

In our case, it will return index 3.

Now, based on the value of q, the division is made.

The array will be divided from 0 to 2 as one half and 4 to 7 as another half.

Again the partition algorithm is called on each sub-problem.

In this way, the array will get arranged in sorted order.