Bubble Sort Algorithm Analysis

For Complete YouTube Video: Click Here

In this class, we will try to understand Bubble Sort Algorithm Analysis.

The prerequisite for this course is the data structures course.

Table of Contents

We have discussed the bubble sorts original data structures and optimized data structures algorithms in data structures.

In this class, we will analyze both algorithms.

We will discuss both algorithms with worst-case and best-case scenarios.

The original bubble sort algorithm is shown below.

In the above algorithm, we have two for loops.

The outer for loop will do n iteration.

The step count of the outer for loop is n.

Every time we enter the outer for loop, the inner for loop will iterate from 0 to n – i -1.

The step count of the inner for loop depends on the value of i.

Analysis of the inner for loop is critical to understanding.

In the first iteration, where the value of i = 0, the inner for loop will iterate for n – 0 -1 times.

Similarly, when the value of i = 1, the inner for loop will iterate for n – 1 – 1 = n -2 times.

When the value of i = 2, the inner for loop will iterate for n – 1 – 1 = n – 2 times.

In the last iteration, the inner for loop will iterate for one time.

If we summarize all the step counts of the inner for loop, it will resemble the sum of n natural numbers.

n + (n – 1) + (n – 2) + …. + 1 = n (n + 1) / 2

If we evaluate the above equation, the higher order term is n².

Now, we will consider the worst and best-case scenarios as shown below.

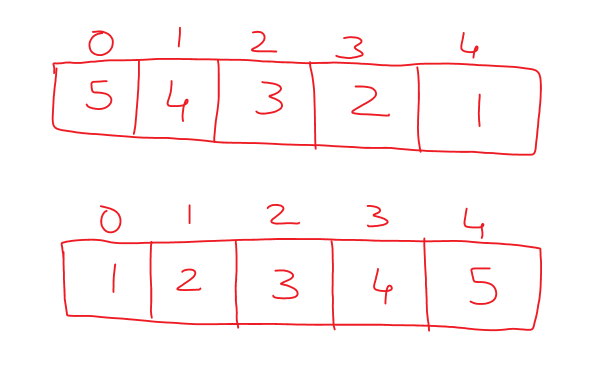
In both cases, the outer and inner for loop will do all the n² iterations.

The algorithm will do all the iterations, so we notate it with theta.

As we have discussed that the original bubble sort will not stop its iteration even if the elements are in the sorted order.

The algorithm for the optimized bubble sort is shown below.

The line marked in red is the changes made to the original algorithm.

Now we consider the worst and best-case scenarios.

In the worst-case scenario, the loop will iterate all n² number of times.

In the best case, where all the elements are in sorted order, the outer loop will iterate only one time.

The inner loop will iterate for n number of times.

After all the iterations, the “swapped” will remain false, and the break will get executed.

In the best-case scenario, the optimized bubble sort will execute for n number of times.