Merge Sort Time Complexity using Recursive Tree Method
For Complete YouTube Video: Click Here
In this class, we will try to understand Merge Sort Time Complexity using Recursive Tree Method.
We have already discussed how to draw a recursive tree in our previous classes.
Merge Sort Time Complexity using Recursive Tree Method
The image below is the algorithm for merge sort.

The image below is the recursive tree for the above merge sort algorithm.
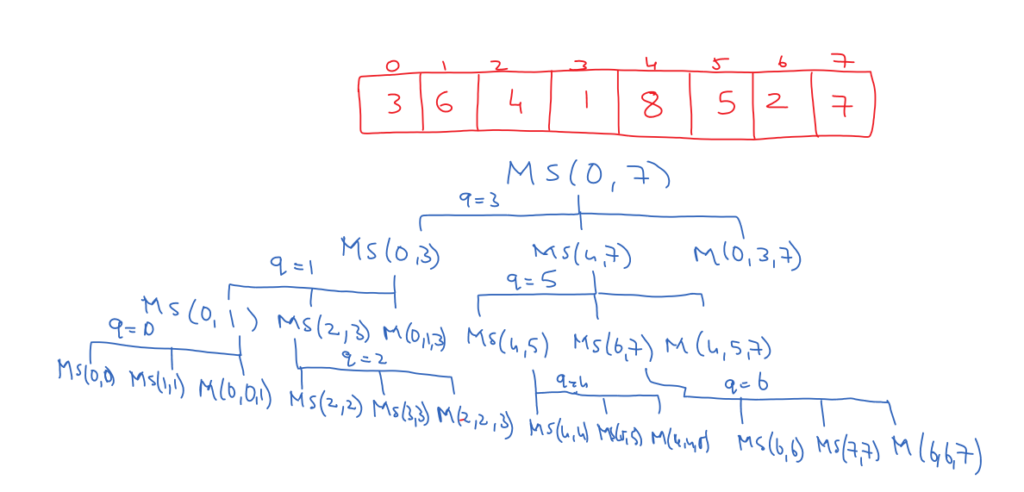
In the above image, MS or Merge-Sort() function is used to divide the array.
The actual sort is made by M or Merge() function.
The step count of the merge function is n.
At level 1, we have a merge function called M(0, 3, 7) on eight elements.
At level 2, the merge functions M(0, 1, 3) and M(4, 5, 7) are called on four elements, and each call means n/2 elements.
On level 2, the merge function is called on eight elements.
Similarly, on level 3 Merge function call is made four times each time the sorting is made on 2 elements.
On level 3, if we combine all the calls, the merge is made on eight elements.
The merge is applied on n elements on each level, and we have three such levels.
Three levels mean log 8, which is 3.
For n elements, we have three or log n levels, and the sorting is made on n elements on each level.
Therefore the efficiency is n log n.
In this way, we can analyze the efficiency of recursive algorithms using the recursive tree method.
