Merge Sort Time Complexity Using Substitution Method
For Complete YouTube Video: Click Here
In this class, we will try to understand Merge Sort Time Complexity Using Substitution Method.
We have already explained the procedure to find the efficiency of an algorithm using the substitution method in our previous classes.
Merge Sort Time Complexity Using Substitution Method
For better understanding, consider the merge sort algorithm as shown below.

Before applying the substitution method, we have to find the recursive equation.
To find the recursive equation, we have to find the time taken by the base part of the algorithm.
The amount of time taken by the base part of the algorithm is one because the algorithm will stop its execution if we have only one element.
Next, we have to find the amount of time taken by the recursive part of the algorithm.
The time taken by the recursive part of the algorithm is T(n) = 2T(n/2) + n.
The image below is the final equation for the merge sort algorithm.
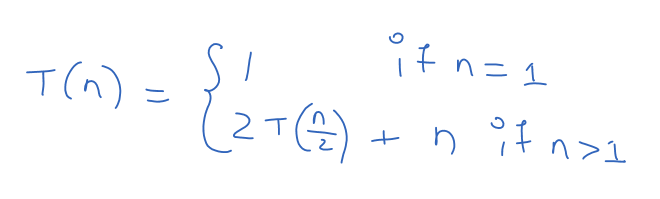
In the above image, the amount of time taken by the merge-sort(p, q) is n/2 because q is the middle value of the array, and using the q value, we can split the array into half.
Similarly, merge-sort(q+1, r) is n/2.
The efficiency of merge(p, q, r) is n.
The step count of each line of code in the merge-sort algorithm is given below.

From the above image, for the merge function, if we sum up all the step counts, the higher order term is n.
Now we will use the substitution method on the above equation and find the efficiency of the merge sort algorithm.
T(n) = 2T(n/2) + n -> (1)
T(n/2) = 2T(n/4) + n/2 -> (2)
T(n/4) = 2T(n/8) + n/4 -> (3)
Substitute equation 2 in 1.
T(n) = 2(2T(n/4) + n/2) + n.
= 4T(n/4) + 2n/2 + n.
= 4T(n/4) + 2n
In the above equation, substitute equation 3.
T(n) = 4(2T(n/8) + n/4) + 2n.
= 8T(n/8) + n + 2n
= 8T(n/8) + 3n
From the above equation, it is clear that T(n) = 2kT(n/2K) + kn.
Now we will consider the base condition.
The algorithm will stop its execution only if n = 1.
If from the equation n/2k = 1.
n = 2k.
k = log n
T(n) = n + n log n.
From the above equation, the higher order term is n log n.
The efficiency of merge sort is n log n.
