Selection Sort Algorithm Analysis
For Complete YouTube Video: Click Here
In this class, we will try to understand Selection Sort Algorithm Analysis.
We discussed the working mechanism and selection sort algorithm and selelction sort algorithm in our data structures course.
The prerequisite for this course is a data structures course.
Selection Sort Algorithm Analysis
The algorithm for selection sort is shown below.

For better understanding, we will consider the following worst-case, average-case, and best-case scenarios.
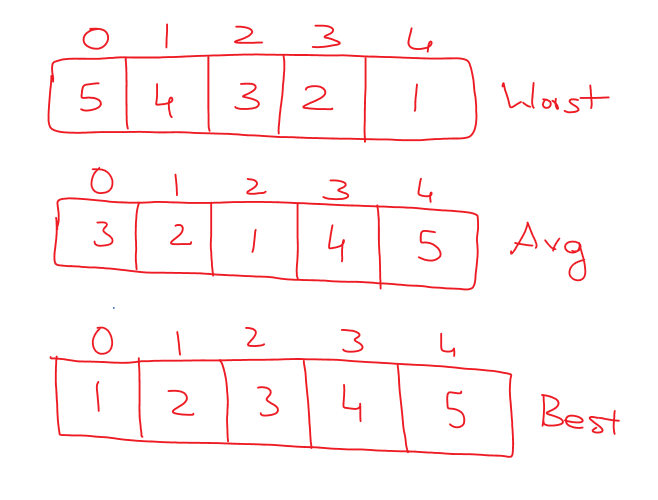
The worst-case scenario means all the elements in the array are in descending order, and we are willing to arrange them in ascending order.
In the average-case scenario the arrangement of numbers radom some are already in sorted orderr and sum or not.
The best-case scenario means all the array elements are in sorted order.
Now consider the first line of the algorithm.
The outer for loop of the algorithm will iterate from 0 to n -2 element of the array.
If the number of elements is five, the outer for loop will iterate from 0 to 3 means four times.
Line one will iterate for n number of times.
The second line of algorithm min = i will execute for n – 1 time.
The following line of code is the start of the inner for loop.
Understanding the behavior of the inner for loop is very important.
The inner for loop will iterate from i + 1 to n.
i + 1 means the iteration of the inner for loop depends on the outer for loops i value.
If the value of i = 0, then the inner for loop will iterate for n times.
If the value of i = 1, then the inner for loop will iterate for n – 1 number of times.
If the value of i = 2, then the inner for loop will iterate for n – 2 number of times.
If the value of i = n – 2, then the inner for loop will iterate for one time.
If we sum up all the terms it will n + (n -1) + (n – 2) + …. + 1.
The above summation is the sum of first n natural numbers.
The equation for the first n natural numbers is n (n + 1) / 2.
If we expand the above equation, the higher order term is n2.
The last line of code will execute n number of times.
If we summarize all the step counts, the higher order term is n2.
The efficiency of the selection is n2.
The n2 number of executions is done for all the above three cases.
Irrespective of the input, whether the values in the array are Worst, average, or best case, the step count is always n2.
Every time the algorithm will run for n2 times.
The asymptotic notation is theta notation.
