Substitution Method

For Complete YouTube Video: Click Here

In this class, we will try to understand the Substitution Method.

We have already discussed the concepts of recurrence relations in our previous class.

Table of Contents

The Substitution Method is used to solve the recurrence relations.

Solving the recurrence relations will produce the efficiency of an algorithm.

To understand this consider the recurrence relation shown below.

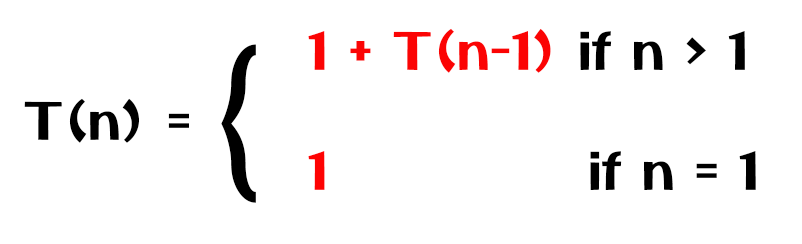
In the above equation, to find T(n)= 1 + T(n-1) – (1), we have to find T(n-1).

To get the value of T(n-1), we have to substitute n-1 in the place of n.

T(n-1) = 1 + T(n-2) – (2).

Similarly, T(n-2) = 1 + T(n-3) – (3).

By substituting the value of T(n-1) in the equation (1), we get T(n) = 2 + T(n-2).

Now substitute the value of T(n-2) in the above equation.

By substituting we will get T(n) = 3 + T(n-3).

The above equation looks like T(n) = k + T(n-k).

This way, we can substitute to any length, but the algorithm will stop executing when the value of n-k = 1.

Now, k = n-1.

Substitute the value k in the above equation.

T(n) = n-1 + T(n – n + 1).

T(n) = n-1 + T(1).

We know from the given equation that T(1) = 1.

T(n) = n.

Therefore the efficiency of the above recurrence equation T(n) = n.