Theta Notation

For Complete YouTube Video: Click Here

In this class, we will try to understand Theta Notation.

The definition of Asymptotic notation, Big O Notation, and Omega Notation was explained clearly in our previous class.

Theta Notation

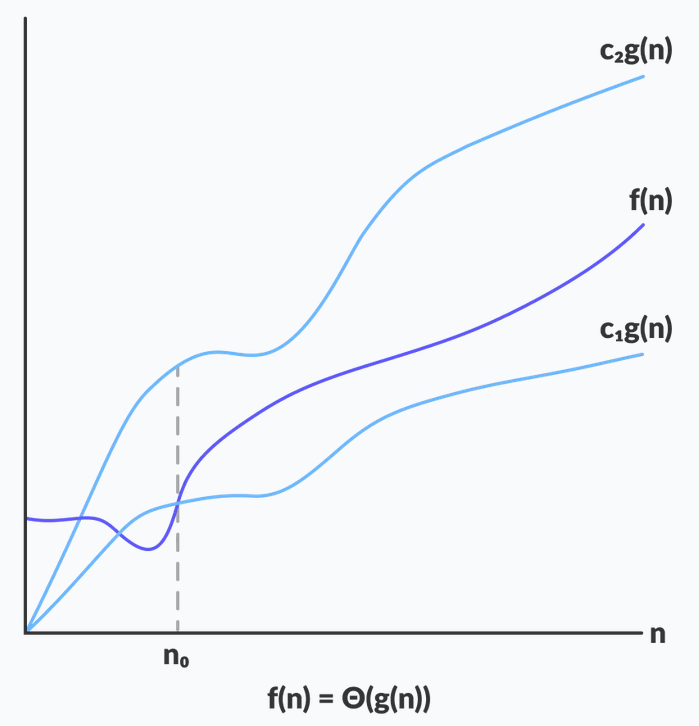
The definition of the Theta Notation is as shown below.

The function f(n) = ɵ(g(n)) if and only if there exists positive constatnts c1. c2 and n0 such that c1*g(n) <= f(n) <= c * g(n) for all n, where n >= n0.

The above definition states that when f(n) is greater than or equal to some constant c1 * g(n) and less than or equal to some constant c2 * g(n) for all the values of n where n is greater than or equal to n0.

This definition is proven for any function f(n). In our course, we consider f(n) as the time complexities of the algorithms.

To understand the definition better, we will consider the example shown below.

For example, the time complexity of an algorithm is 3n + 2.

This 3n + 2 can be expressed in Theta notation if we can prove that 3n + 2 is greater than or equal to c1*g(n) and less than or equal to some constant c2*g(n) for all the values of n where n >= n0.

Consider 3n <= 3n + 2 <= 4n for all the values of n >= 2 (n0 = 2).

The above expression is valid for all the values of n >= 2.

If n = 2 then 3n <= 3n + 2 <= 4n is true.

If n = 3 then 3n <= 3n + 2 <= 4n is true.

Simillarly, for n = 10, 3n <= 3n + 2 <= 4n is true.

In such cases, we can say that 3n + 2 = ɵ(g(n)).

How does the Theta notation describe an algorithm?

We will get the exact bound for the function with the Theta notation.

For all the values of n >= 2, 3n + 2 will always be inbetween 3n and 4n.

The image below shows the Theta notation on a graph.

For a clearer and better understanding, click on the top and learn for free.