Types of Order of Growth of an Algorithm

For Complete YouTube Video: Click Here

This class will try to understand the Types of Order of Growth of an Algorithm.

We have already discussed the concept of Order of Growth in our previous class.

Types of Order of Growth of an Algorithm

Different Types of Order of Growth of an Algorithm we come across in this course are shown below.

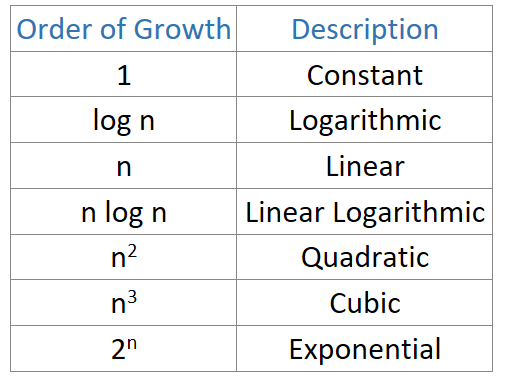
The terms order of growth, the efficiency of an algorithm, or the number of steps executed by an algorithm means the same.

Constant Order of Growth (1)

The constant order of growth means the number of steps executed by the algorithm is constant, whatever the input may be.

For example, if an algorithm input is 10 or 100 or 1000, the number of steps executed by that algorithm is always constant.

Logarithmic Order of Growth (log n)

The Order of Growth of these algorithms is logarithmic.

For example, if the algorithm input is 8, the number of steps executed by this algorithm is log 8 (which means three steps are performed to get the output).

Linear Order of Growth (n)

The Linear Order of Growth means the number of steps executed by an algorithm is same the as the size of the input.

For example, if the inputs are 10 or 100 or 1000, the algorithm executes those many numbers steps.

Linear Logarithmic (n log n)

The Order of Growth of these algorithms is linear logarithmic.

For example, if the input 8 means the number of steps executed is 8 * 3 = 24.

Quadratic Order of Growth (n²)

The Order of Growth of the Algorithms is Quadratic means. For example, ten inputs mean the number of steps executed is 100.

Cubic Order of Growth (n³)

The Order of Growth of the Algorithms is Quadratic means. For example, ten inputs mean the number of steps executed is 1000.

Exponential Order of Growth (2ⁿ)

The Order of Growth of the Algorithms is Quadratic means. For example, ten inputs mean the number of steps executed is 1024.

From the above table, as we move down from constant to exponential, the efficiency of the algorithms will decrease.