Complex Regular Expression Example

For Complete YouTube Video: Click Here

In this class, We discuss Complex Regular Expression Example.

The reader should have prior knowledge of regular expression to finite automata. Click Here.

Take an example and understand how we write complex regular expressions.

Example 1: The set of strings contain 110 as substring over the alphabet Σ = {0,1}.

The above language is not a complex language. We refresh the concept to understand the next example.

The regular expression for set of strings having 110 as substring is (0 + 1)*110(0 + 1)*

Before we find 110, we can accept any string, so we write (0 +1)* before 110.

After 110, we can accept any string, so we write (0 +1)* after 110.

Example 2: The set of strings not containing 110 as substring.

This example is a bit complex to write a regular expression.

Logic: After finding two consecutive ones, we should not find zero. Based on the logic we need to write an expression.

Try different combinations.

First: (0 + 1) *

The regular expression (0 + 1) * can generate the string 110.

We try another combination.

Second : (0 + 11)*

The regular expression (0 + 11)* can also generate the string 110.

Third : (0 + 01)*1*

The regular expression (0 + 01)*1* will not generate the string 110.

Let’s understand the expression.

the expression (0 + 01)* will take either 0 or 01. any number of times.

The strings generated by (0 + 01)* are {ε, 0, 01, 001, 0101, . . .}

Two consecutive ones is not generated by the expression (0 + 01)*.

Whenever we find two consecutive ones, we are not allowed to generate zero, sequence of ones is allowed.

So we added 1*, to the expression.

The final expression is (0 + 01)*1*.

The expression (0 + 01)*1* not going to generate the string 10. We accept the string 10 in our language.

So example three is not suitable for our language.

We go with another combination.

Example 4: (0 + 10)*1*

The regular expression (0 + 10)*1* will generate the string 10 and not generate the string 110.

Checking all the possibilities is not easy to write the regular expressions.

So in this situation we go with alternative method.

We write DFA for the language and convert to regular expression using ardens method. Click Here.

The below diagram shows DFA to accept 110 as substring.

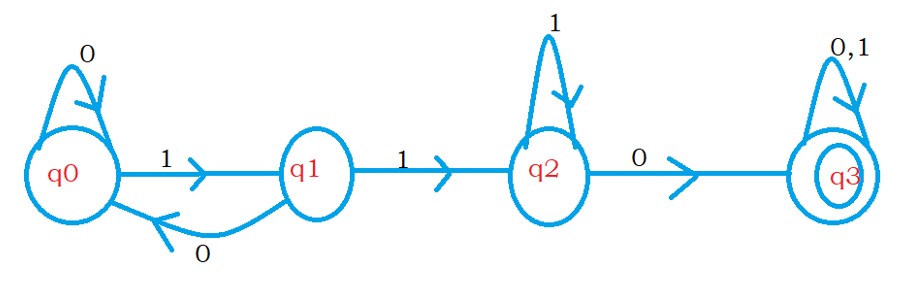
We change final states to non final and non final to final to get the DFA not having 110 as sub string

The below diagram shows the DFA that do not accept 110 as sub string.

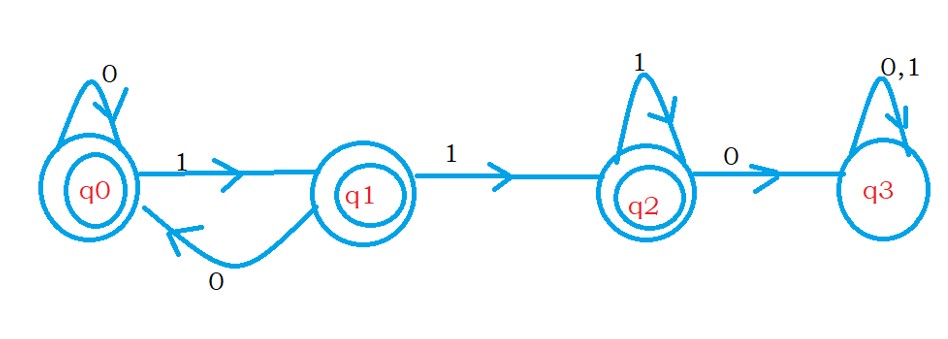
Now convert the DFA to regular expression using ardens method.

First write the equation for all the states.

q0 = q00 + q10 + ε

q1 = q01

q2 = q11 + q21

q3 = q20 + q3(0 + 1)

Substitute q1 in q0.

q0 = q00 + q010 + ε

q0 = q0(0 + 10) + ε

q0 = (0 + 10)*

q1 = (0 + 10)*1

q2 = (0 + 10)*11 + q21

q2 = (0 + 10)*111*

The final expression is (0 + 10)* + (0 + 10)*1 + (0 + 10)*111*

The minimized expression is (0 + 10)*1*. The minimization process is discussed in our next classes.

The same equation we defined in the above explanation.