Context Free Grammar and Language

In this class, We discuss Context-Free Grammar and Language.

For Complete YouTube Video: Click Here

The reader should have prior knowledge of grammar. Click Here.

We refresh the concept of grammar and move to context-free grammar.

Grammar: We represent grammar using four tuples.

G = {V, T, P, S}

V means set of variables. We call them nonterminals.

T means set of terminals

P means set of productions

S is the start symbol

Right Linear Grammar:

Conditions for right linear grammar are left side we should have nonterminal and right side terminal followed by no terminal or single terminal.

The below grammar is an example of right linear grammar.

S – aA| aB| a

A – bA | bB

Left Linear Grammar:

Conditions for Left linear grammar are left side we should have nonterminal and right side nonterminal followed by a terminal or single terminal.

The below grammar is an example of Left Linear Grammar.

S – Aa| Ba| a

A – Ab | Bb

Context-Free Grammar:

We represent context-free grammar using four tuples G = {V, T, P, S}

The production conditions are different.

Production conditions:

Conditions for context-free grammar are left-side single nonterminal, and right side, we have a string of terminal and nonterminals.

The below grammar is an example of context-free grammar.

S – aAbS

Here lower case characters are terminals, and upper case characters are nonterminals.

Context-free Language: A language for which we can define context-free grammar. We call it context-free language.

Example: L = {aⁿbⁿ where n >= 0}

The below grammar shows the context free grammar for the language L = {aⁿbⁿ where n >= 0}.

S – aSb

S – ε

How to write context-free grammar for a given language? We discuss this in our following classes.

Important to Understand:

Regular grammar is a subset of context-free grammar.

Take any right linear or left linear grammar. Those are a subset of context-free grammar.

In context-free grammar right side of the production can have a string of terminal and nonterminals.

Right linear grammar will have terminal followed by nonterminal productions.

RLG conditions are a subset of CFG production conditions.

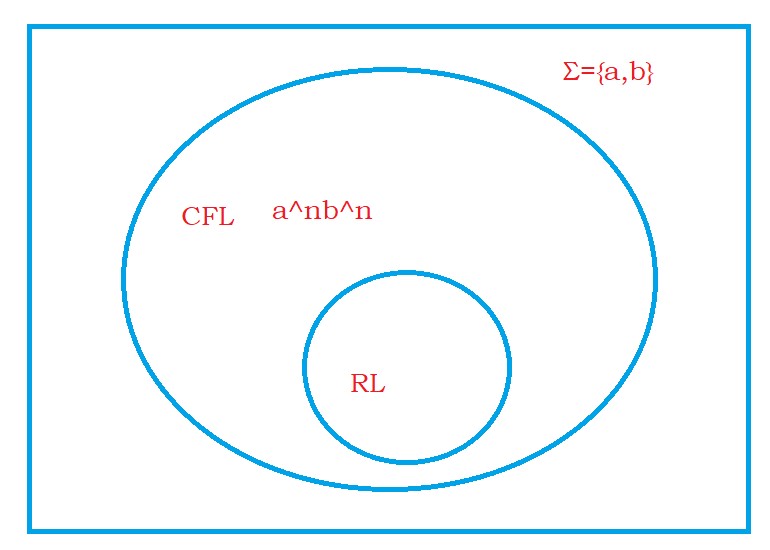
The below Venn diagram is important.

The rectangular box contains a set of all the languages defined using alphabet Σ = {a,b}.

Out of all the languages, some of the languages are defined using regular grammar. We call those languages regular languages.

The inner circle shows the regular languages.

The outer circle shows the context-free languages.

The regular languages are a subset of context-free languages is shown in the Venn diagram.