CYK Membership Algorithm

In this class, We discuss CYK Membership Algorithm.

For Complete YouTube Video: Click Here

The reader should have prior knowledge of Context-Free Grammar. Click Here.

We use the CYK algorithm to check the given input string is accepted by CFG or not.

Example:

S – AB | BC

A – BA | 1

B – CC | 0

C – AB | 1

The input string is 01101.

The length of the input string is 5. so we take five columns and five rows and construct the matrix.

The below-given matrix shows the final output. From the matrix, we identify the given input string is accepted or not.

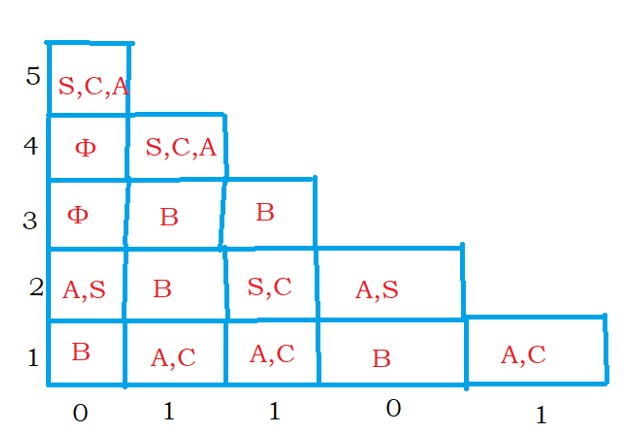
The rows are numbered 1 to 5.

First step: Convert the given CFG to the form CNF.

The given CFG is in the form of CNF.

Second step: Identify all possible single-length strings from the input.

0 is one of the possible single-length strings from the input.

From the given CFG. We can determine 0 using B.

In the first row above 0, we placed the value B.

Similarly, one can be determined using A, C.

In the first row, we place A, C where one is present in the column.

In the second row, we place possibilities of two long strings.

In the third row. We place possibilities of three length strings. And so on.

The possible two-length strings are 01, 11, 10,01.

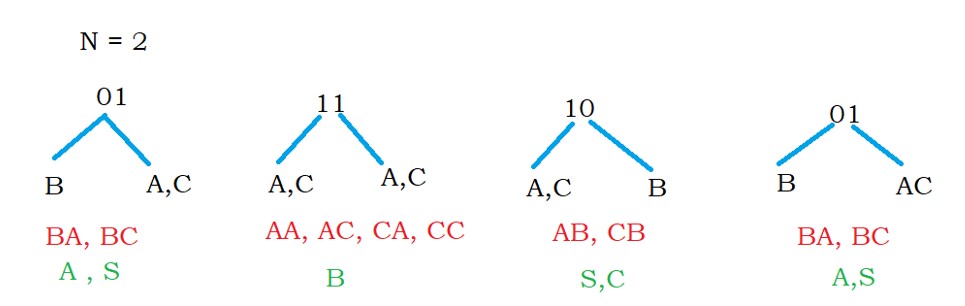
We have to take sequential possibilities from the input string 01101.

From left to right input string, we have 01, 11,10,01 are the four possible two-length strings.

Take 01

0 is determined using B, and one is determined using A, C.

so 01 can be determined using BA and BC.

The given CFG BA is determined using A, and BC can be determined using S.

The possibility of string 01 is S, A.

We have written this in the second-row first column.

Similarly, we do for the remaining two-length possible strings.

Similarly, we can determine 11 using B.

10 can be determined using S, C.

01 can be determined using S, A.

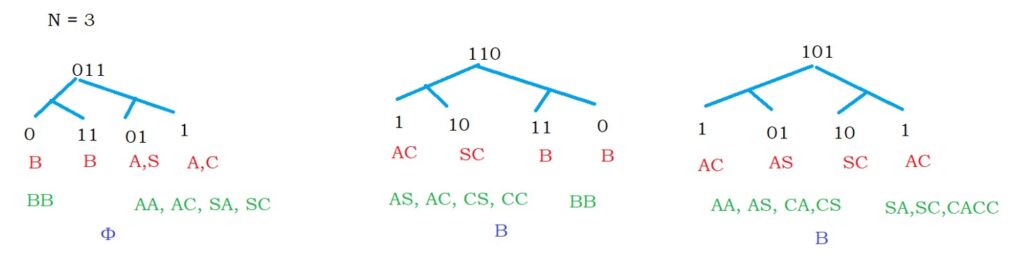
Now we determine all three length strings.

The possible three-length strings are 011, 110, 101.

The possibilities of 011 are

0 can be determined using B, and 11 can be determined using B.

011 can be determined using BB.

The possibility BB is not in CFG.

The other possibilities are

01 can be determined using A, S. and one can be determined using A, C.

The combinations are AA, AC, SA, SC.

Above all, combinations can not be derived using the given CFG.

So we can not determine the string 011. We have written as Φ.

The below diagram shows all the three-length strings possibilities.

Similarly, we do for four and five-length strings.

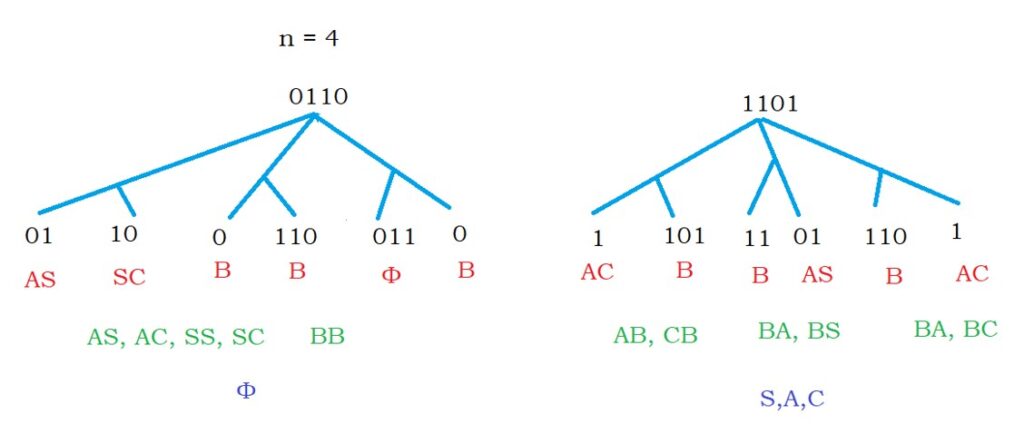
Finally, in the fifth row, we got the start symbol S.

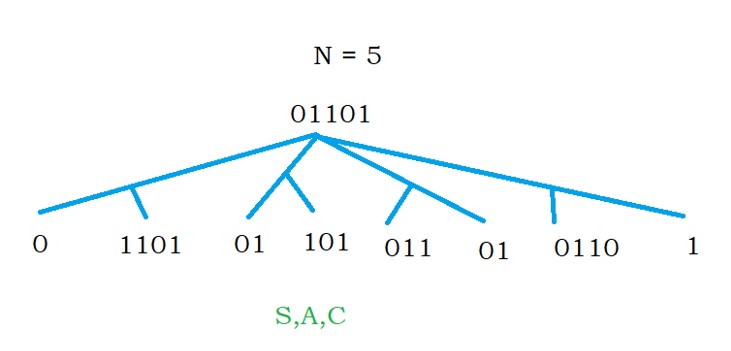
The given string is accepted because we derive the start symbol S in the fifth row.

We can derive the input string from the start symbol S.