Deterministic Finite Automata

For Complete YouTube Video: Click Here

In this class, We discuss Deterministic Finite Automata.

The reader should have prior knowledge of introduction to Formal languages and automata theory. Click here.

The below shown diagram is discussed in our previous class. we use the example to understand finite automata.

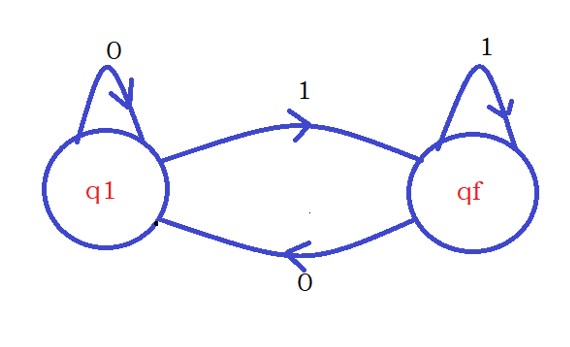
Before we understand deterministic finite automata. First, we discuss finite automata.

Finite Automata

A automata is a machine/device take some input and do some functions with out the involvement of a man we call it automata.

The above shown diagram we call it finite automata. because we showed in our previous class how we convert the above diagram into device or machine that process the strings with out involvement of man.

Here finite means finite number of states.

A finite automata can be defined using a five tuple. M={Q,Σ,q0,F,δ}.

Q is finite set of states.

In our above example we have two states q1 and qf.

Σ is finite set of input symbols.

In our example we have input symbols 0 and 1.

q0 is the initial state.

In our example q0 = q1. q1 is our initial state. we start from the state q1.

F is finite set of final states. In our example we have one final state qf.

We can have any number of final states. F⊆Q.

F is always subset of Q. because some of the states are considered final.

δ is the transition function. we represent transition function as δ: QXΣ->Q.

Example: q0X0 -> q0

On the state q0 we see the input symbol 0 and moved to the state q0.

The movement of the automata is shown using transition function.

We can represent the complete transition in two ways.

Transition Diagram:

In the transition diagram initial state is give using arrow. and the final state is mentioned using double circle.

The above diagram is the transition diagram.

Transition Table:

Deterministic Finite Automata

A deterministic finite automata is a finite automata. Which follows two conditions.

First condition: Every input symbol should have a transition on every state.

In our example take the state q1. On the state q1 we have a transition for input symbol 0 and transition for input symbol 1.

Similarly, on the state qf.

Second Condition: When we apply a transition on the input symbol, The transition should move to exactly one state.

The below example moves to two states after applying the input symbol 1. This is not allowed in DFA.

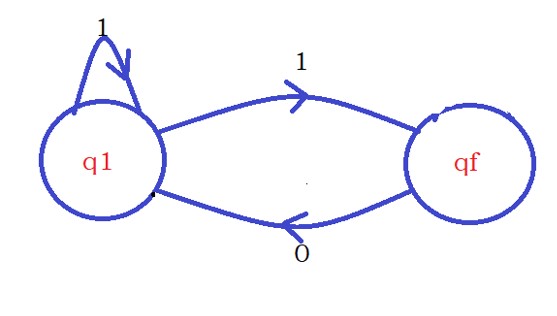
If the above two conditions are satisfied we call it deterministic finite automata.