DFA Example on Counting 1

For Complete YouTube Video: Click Here

In this class, We discuss DFA Example on Counting 1.

The reader should have prior knowledge of counting examples. Click here.

First Example: Design DFA That accepts strings containing four zeros and atleast two ones.

The input symbols are Σ={0,1}.

Counting four zeros logic was discussed in our previous classes.

Similarly, logic to check atleast two ones is also discussed.

We need to combine both the logic.

The below diagram shows the complete DFA.

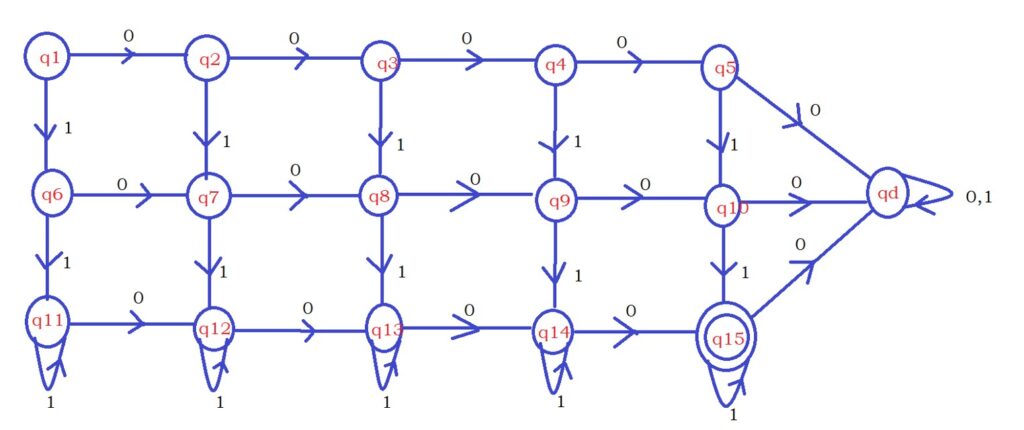
The horizontal layer identifies the four zeros.

The vertical layer identifies atleast two ones.

Because the zeros are counted, and they need not be consecutive. The logic is complex.

For understanding, we are explaining the example in layers. DFA does not have layers.

Whenever we see one zero in our input string, we end up in the second vertical layer.

Example: 101 string we end up in state q12.

Similarly, if we encounter one, we end up in a second horizontal layer.

After seeing four zeros, we end up in the fifth vertical layer. More than four zeros go to a dead state because we need to accept strings having four zeros.

After seeing two ones, we can ignore to check ones because logic is atleast two ones. So we stay in the same state.

Second Example: Design DFA to accept all strings of length atmost 5.

The input symbols are Σ={0,1}.

The first input character can be 0 or 1. so we move to state q1.

Similarly, we move to the first five characters.

Given atmost five, so we can accept strings of length 0,1,2,3,4,5.

We make the first six states final because we accept of length atmost 5.

After five characters still string is there, we move to a dead state.