DFA Example on Counting 2

For Complete YouTube Video: Click Here

In this class, We discuss DFA Example on Counting 2.

The reader should have prior knowledge of counting examples. Click here.

First Example: Design DFA that accepts strings contain even no of zeros and ones.

The input symbols are Σ={0,1}.

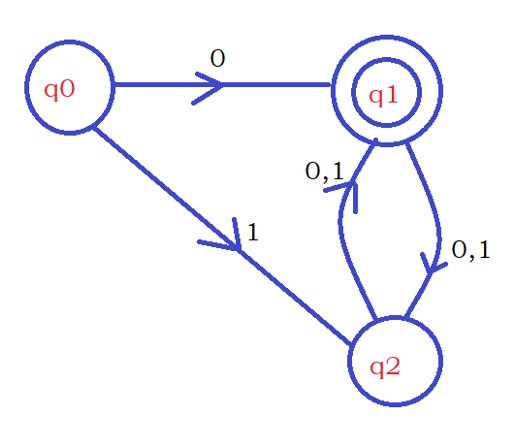
In our previous classes, we designed a DFA that accepts strings containing an even number of zeros.

The below diagram shows the logic of DFA accepts a string containing an even number of zeros.

In this example, we need to find strings that contain even zeros and ones.

So we go with a layered approach because conditions are applied on both zeros and ones.

The layered approach example is discussed in our previous class.

The below diagram shows the DFA accepting strings having an even number of zeros and ones.

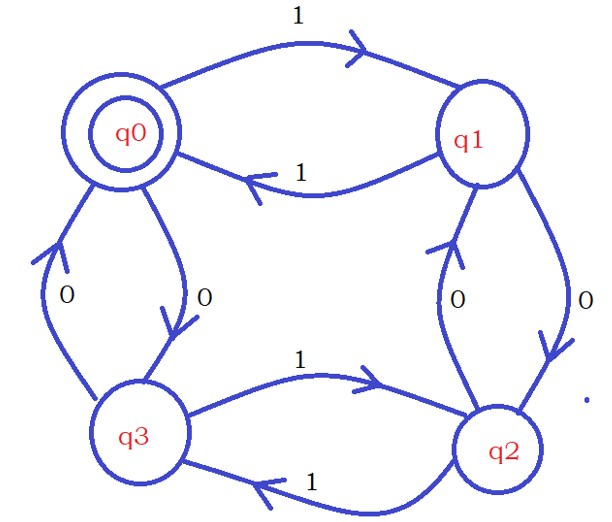
Whenever we have an odd number of ones in the string, we end up in the second vertical layer.

Similarly, if the string contains an even number of ones, we end up in the first vertical layer.

Whenever we have an odd number of zeros, we end up in the second horizontal layer.

Similarly, if the string contains an even number of zeros, we end up in the first horizontal layer.

The state q0 is considered the final state because the intersection of even number of zeros horizontal layer and even number of ones vertical layer is q0.

We can use the same diagram to find the other logic.

For example, Design DFA accepts strings containing an even number of zeros and an odd number of ones.

Check the intersection of the two conditions mentioned and make the state final.

In this example, state q1 should be made final.

Second Example: Design DFA that accepts strings that start with zero and have even length strings. And start with one and have an odd length string.

The input symbols are Σ={0,1}.

The first input character is 0. We need one logic. If it is one, we need other logic.

Similar examples having or conditions between two logic are explained previously. Click here.

On the state q0, If we encounter the input character 0, we move to q1.

Similarly, if we see the input character 1, we move to state q2.

After seeing input character zero, we need to count the length of the string, and it should be odd.

The logic to count even length is discussed previously.

So we made q2 as the final state because we end up in state q2 if the odd length string and starting character are zero.

Similarly, we end up in state q2 if even length string and starting character are one.