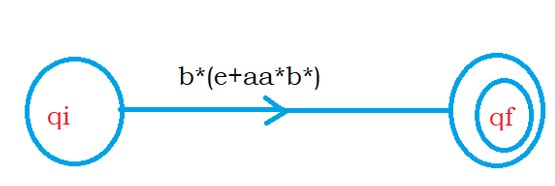DFA to RE State Elimination Multiple Final and Dead State Example
For Complete YouTube Video: Click Here
In this class, We discuss DFA to RE State Elimination Multiple Final and Dead State Example.
The reader should have a prior understanding of DFA to the regular expression process. Click here.
Example 1:
The below diagram is a DFA containing multiple final states and a dead state.
In the diagram dead state is C. because after reaching state C, we are staying in C.
We can remove the dead state.
The below diagram shows the finite automata after removing the dead state.
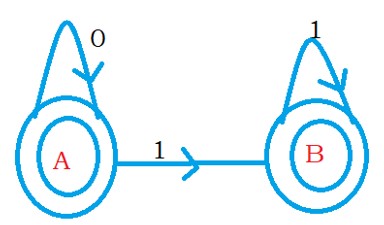
The initial state A has the incoming edge. And we have multiple final states.
We need to add a new initial state and a new final state.
The below diagram shows the finite automata after adding the initial and final state.
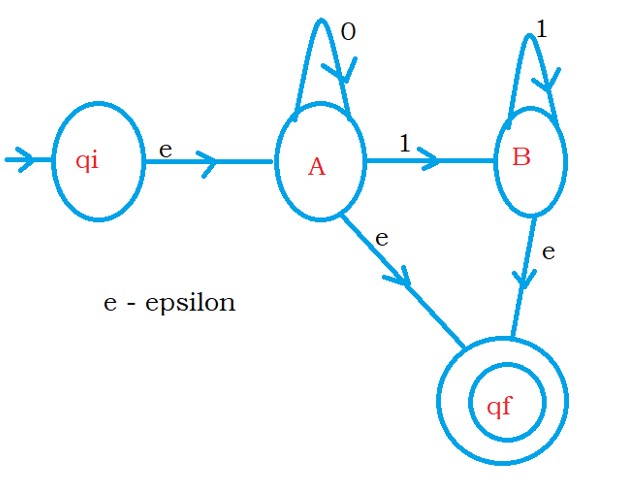
First, we eliminate state B.
If we eliminate state B, we move from state A to state qf using 11*.
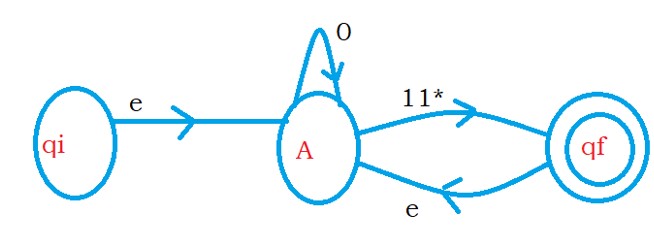
We have another transition to state qf from state A using epsilon moves.
So we write a transition from state A to state qf as (ε + 11*)
We minimize the equation to 1*.
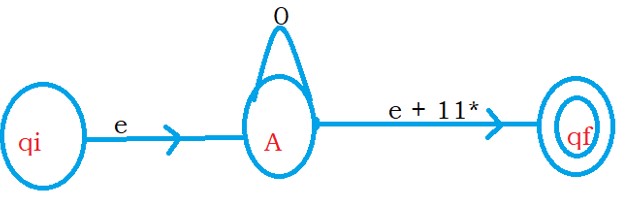
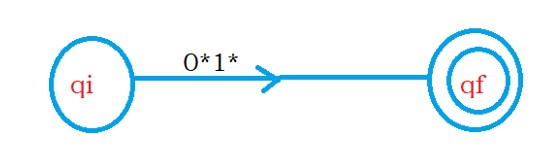
If we eliminate state A, the final regular expression from State qi to state qf is 0*1*. Because self-loop with input zero on state A.
Example 2:
We take one more example for better practice.
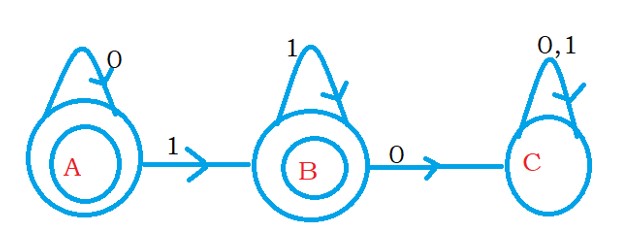
The below diagram shows the DFA with multiple final states and dead states.
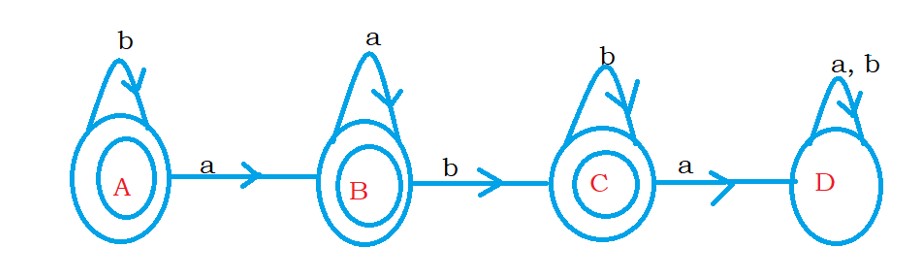
State D is a dead state, so that we can remove the state.
The initial state A has incoming edges, and we have multiple final states.
We need to add a new initial state and a new final state.
The below diagram shows the finite automata after adding initial and final states.
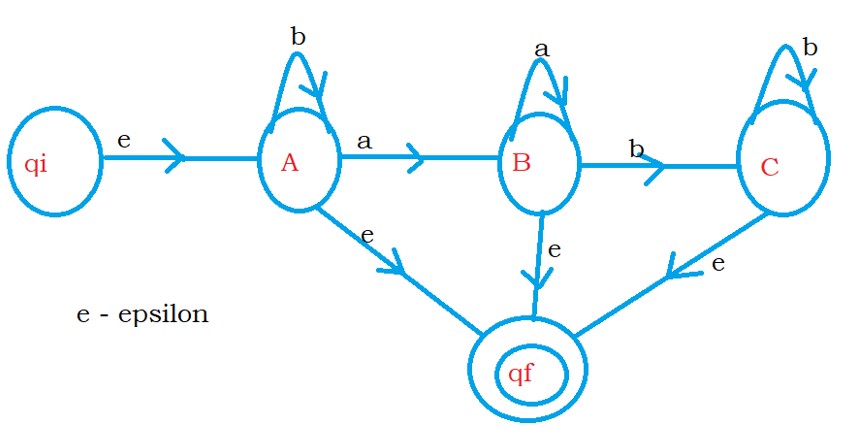
First, we remove state C. after removing state C. We move from state B to state qf using bb*.
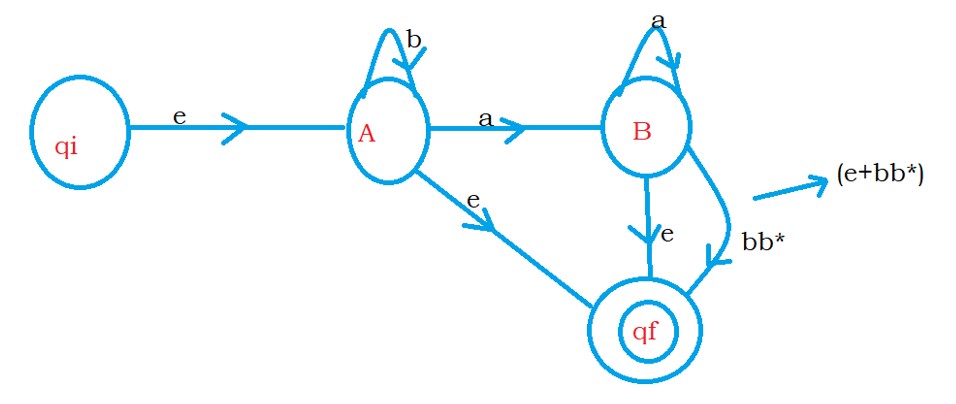
We have one more transition from state B to state qf using epsilon.
So we write the transition as (ε + bb*). We minimize to b*.
Now we eliminate state B.
After eliminating state B, we reach from state A to state B using (ε + aa*(b*))
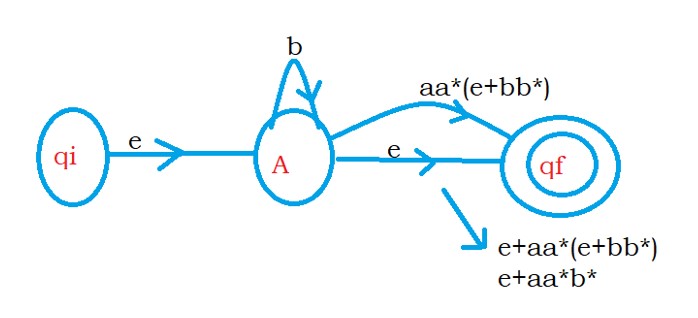
Now we eliminate state A.
After eliminating state A, we remain with the final regular expression b*(ε + aa*(b*)).