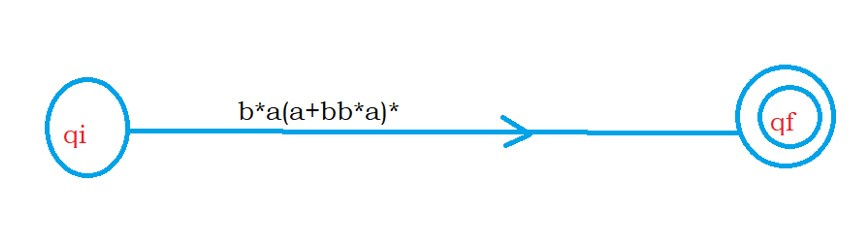DFA to Regular Expression State Elimination Method

For Complete YouTube Video: Click Here

In this class, We discuss DFA to Regular Expression State Elimination Method.

The reader should have prior knowledge of regular expressions. Click Here.

We follow the steps for the state elimination method.

Step 1:

If there exists any incoming edge to the initial state, add a new initial state.

Example:

The below diagram has an incoming edge to the initial state.

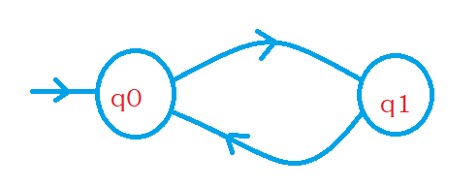
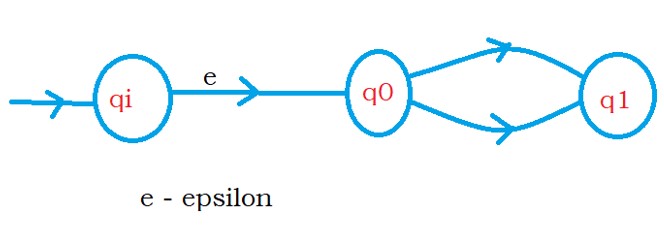
Add a new state qi and move to state q0 using epsilon moves. Make qi as the initial state.

The below diagram shows the final diagram after adding a new initial state.

Step 2:

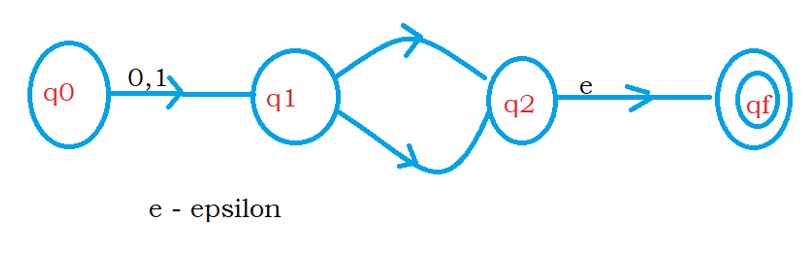
if there exists an outgoing edge to the final state, then create a new final state.

Example:

The below diagram has an outgoing edge to the final state.

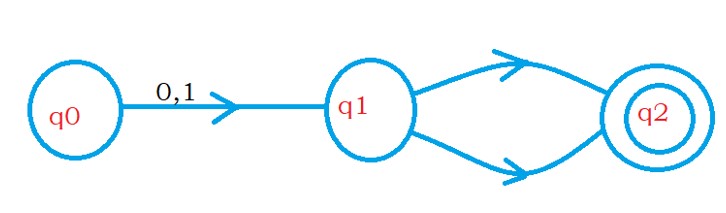
We add a new final state qf, and make q2 as the non-final state.

From state q2, we move to qf using epsilon moves.

The below diagram shows the final diagram after adding a new final state.

Step 3:

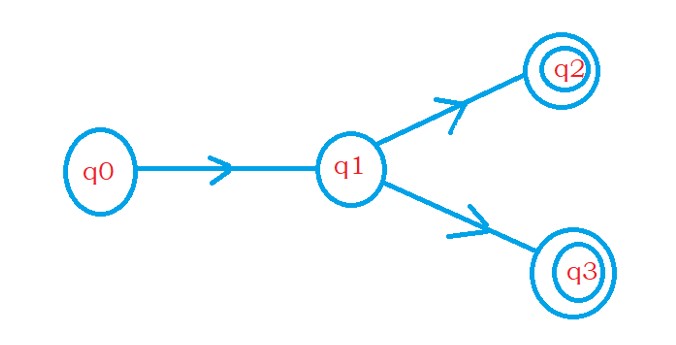
if there exist multiple non-final states, make them non-final and create a new final state.

The below diagram has two final states q2 and q3.

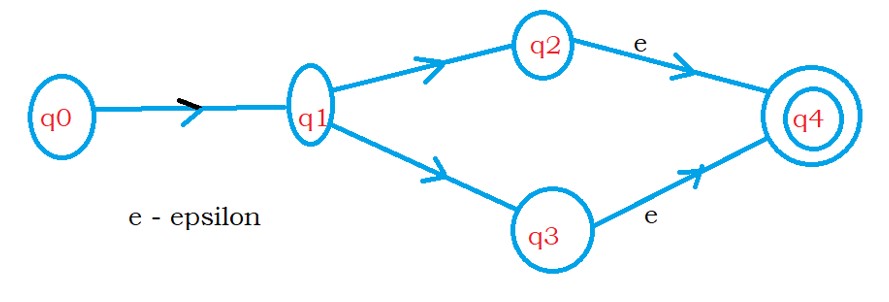
We change q2 and q3 as non-final states and add a new final state qf.

The states q2 and q3 are joined to qf using epsilon moves.

The below diagram shows the modifications.

We understand a few examples.

Example 1:

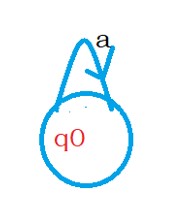
The regular expression for the DFA is a*.

Example 2:

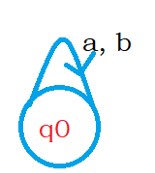
The regular expression for the DFA is (a + b)*

We take a or b. We stay on state q0, and we can repeat any number of times.

Example 3:

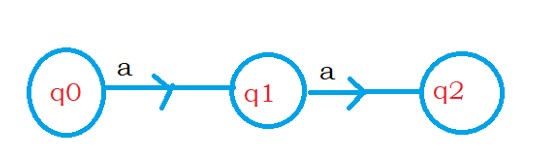
The regular expression for the DFA is aa.

Example 4:

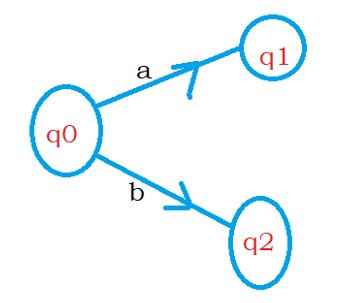
The regular expression for the DFA is (a + b)

Example 5:

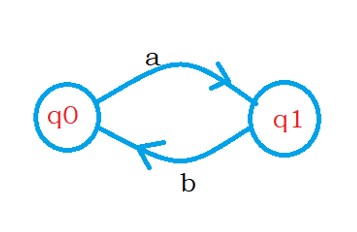
The regular expression for the DFA is (ab)*. We form a cycle with ab.

Now we take an example and find the regular expression using the state elimination method.

The below diagram is our DFA.

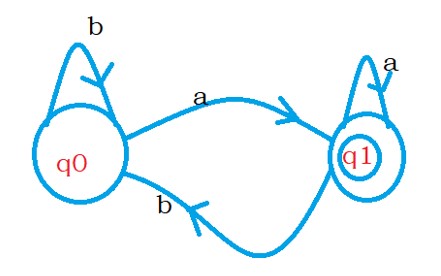
For the DFA, we need to add a new initial state and final state because the initial state has an incoming edge. And the final state has an outgoing edge.

The below diagram shows the final automata after adding the initial and final state.

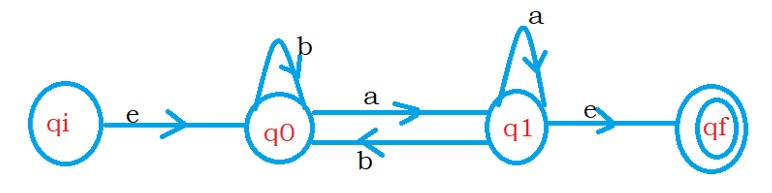
Now we need to eliminate the states between initial and final states.

We can follow any order. We can eliminate q0 first, then q1 or vice versa.

Any order of elimination will give the same output expression.

We eliminate q0 first.

The below diagram shows the Finite automata after eliminating q0.

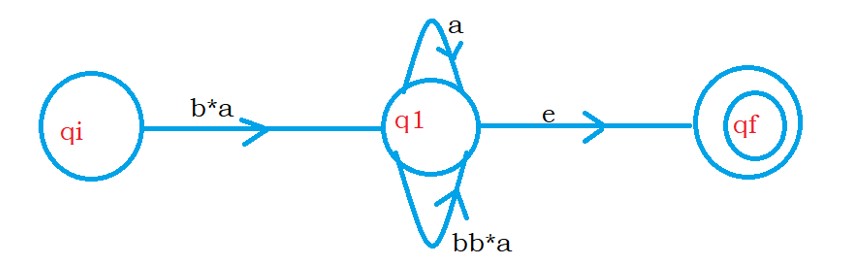
From state qi to state q1, we move using the expression b*a.

with input b, we move to state q0, and with a, we move to state q1.

Point to understand: we have input edge from state q1 to q0. after eliminating q0, we need to take care of that edge.

So on q1, we write a self-loop with the expression bb*a.

Now we have to eliminate state q1.

State q1 has two self-loops. So we use or condition.

If we eliminate state q1, we get the expression (a + bb*a)*

The final regular expression between state qi and qf is b*a(a + bb*a)*. Because q0 is having self loop.