DFA to Regular Expression Using Ardens Theorem

For Complete YouTube Video: Click Here

In this class, we discuss DFA to Regular Expression Using Ardens Theorem.

The reader should have a prior understanding of regular expressions. Click Here.

First, we understand the ardens equation.

R= Q + RP

R= QP*

If the equation is of R= Q + RP, we can write it as R= QP*.

We are not going into the proof of the equation.

We take an example and understand how to use ardens equation to convert DFA to a regular expression.

Example 1: The below diagram shows the DFA.

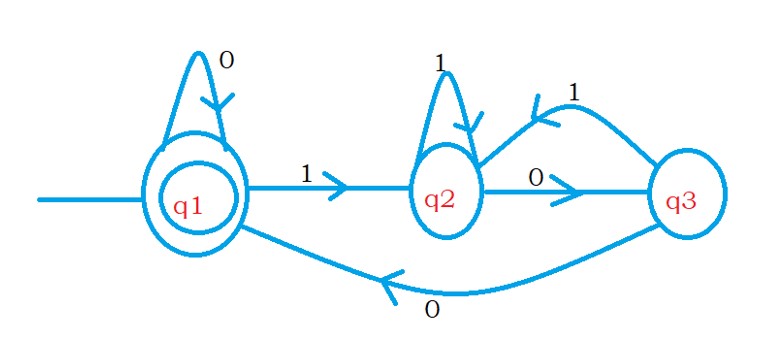
In the DFA, we have three states.

First step:

We have to write the equations of each state.

Take the state q1 and write all the input edges to state q1.

q1 = q10 + q30 + ε

Understand the above equation.

on state q1 if we apply input symbol zero we are moving to state q1. so we have incoming edge on q1.

on state q3 if we apply input zero we are moving to state q1. so we have incoming edge on q1.

We add epsilon to initial state. because we start with initial state with out input we can be on initial state.

Similarly write equation for q2 and q3.

q2 = q11 + q21 + q1

q3 = q20

Now we go with substitution method

Substitute q3 in q2.

q2 = q11 + q21 + q201

Take q2 common

q2 = q11 + q2(1 + 01)

The above equation is of the form R = Q + RP

R = q2

Q = q11

P = (1 + o1)

So we write as R = QP*

q2 = q11(1 + 01)*

Using substitution solve equation q1.

q1 = q10 + q30 + ε

q1 = q10 + q200 + ε

q1 = q10 + q11(1 + 01)*00 + ε

q1 = q1(0 + 1(1+01)*00) + ε

The above equation is of the form R = Q + RP

Q = ε

R = q1

P = (0 + 1(1+01)*00)

we write it as R = QP*

q1 = (0 + 1(1+01)*00)*

We consider q1 = (0 + 1(1+01)*00)* as our final regular expression. because q1 is the final state.

The final regular expression is (0 + 1(1+01)*00)*.