DFA with Dead State Example

For Complete YouTube Video: Click Here

In this class, We discuss DFA with dead state example.

The reader should have prior knowledge of previous examples. Click here.

To construct the DFA on your own, please follow our first ten classes.

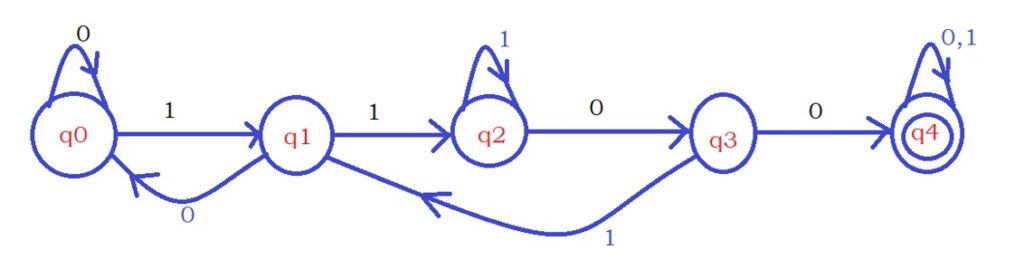
First Question: Design DFA, which accepts string 1100 only.

The input symbol is Σ={0,1}.

In our previous class, we discuss logic to construct DFA accepting strings with the last two characters 1.

Whenever we find two consecutive ones, we move to the final state.

Similarly, we need to find the string with consecutive 1100, so the diagram below will consider logic to take consecutive 1100.

After finding the string 1100, we are moving to the final state.

The above mentioned is the base logic to construct DFA.

Now we add the remaining logic conditions one by one.

On the state q0, if we have seen the input character one, we are moving to state q1.

Suppose we find the input character 0 on state q0. Then we are moving to dead state qd.

Why do we call it a dead state?

Because if we find the first character zero. Then no need to check the remaining logic.

In the situation mentioned above, we move to a dead state.

On the dead state, whatever the input character found, we remain on the dead state because no need to check the logic.

Similarly, if we encounter the input character zero on the state q1, we move to a dead state.

On the remaining states, q2 and q3, the same logic applies.

Point to understand: we consider a dead state when there is no need to check the logic.

The below example shows the complete DFA diagram.

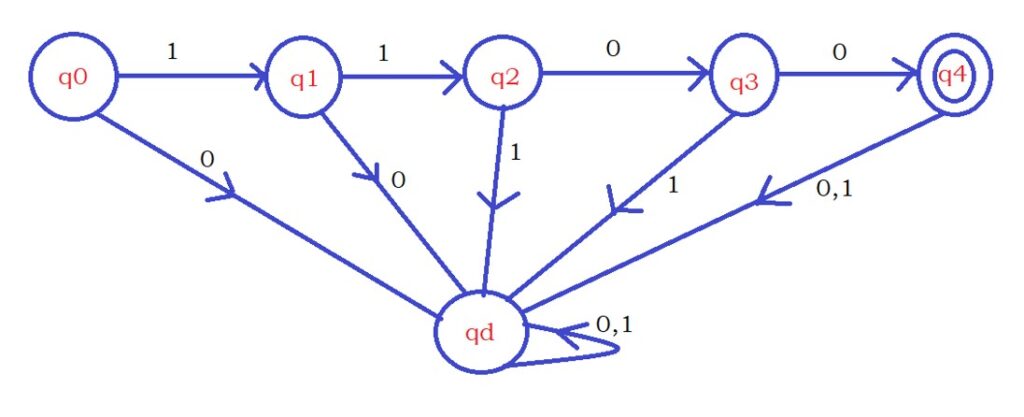
Second Question: Design DFA, which accepts a set of all strings contain 1100 as a substring.

The base logic is similar to the above question. We need to find consecutive 1100.

Whenever we find the consecutive 1100 in the string, we move to the final state.

The below diagram shows the base logic.

From the base logic, we need to construct the remaining conditions one by one.

On the state q0, if we find the input character zero. We stay in the same state because we are not making any condition in 1100.

We start our logic from state q0. Whenever we see input character one, we move to state q1 because we take one step in the required string 1100.

On the state q1, if we find the input character 0, we are moving to state q0 because we lost the required logic.

We need to check our required logic from the beginning on the next encountered input characters.

On the state q2, when we encounter the input character one, we stay in the same state. Because we still have the last two characters’ ones.

We move to state q2 whenever we find two consecutive ones.

After finding two consecutive ones again, if we encounter one, we are not losing the logic of two consecutive ones. so we stay on state q2.

On the state q3, if we encounter input one, we move to state q1.

We move to state q3 whenever we encounter consecutive 110. After finding 110, if we encounter the input character one, we lose the required logic.

So we are moving to state q1 because the present input character allows us to take one step required.

On the state q4, we can stay on state q4 when we see any input character.

We move to state q4 whenever we see consecutive 1100. we had seen the sub-string 1100.

After finding the sub-string 1100, we can remain on the state qf because the string is accepted.

The below diagram shows the complete DFA.