DFA with Dead State Example 1
For Complete YouTube Video: Click Here
In this class, We discuss DFA with Dead State Example 1.
The reader should have prior knowledge of DFA with dead state examples. Click here.
First Example: Construct DFA that accepts strings starting with aa or bb.
The input symbols are Σ {a,b}.
In this example, we need to check to start with aa or bb.
Two options are there. And any one of the options can be satisfied.
Check the below diagram, we are checking aa condition, and on the other side, we are checking bb condition.
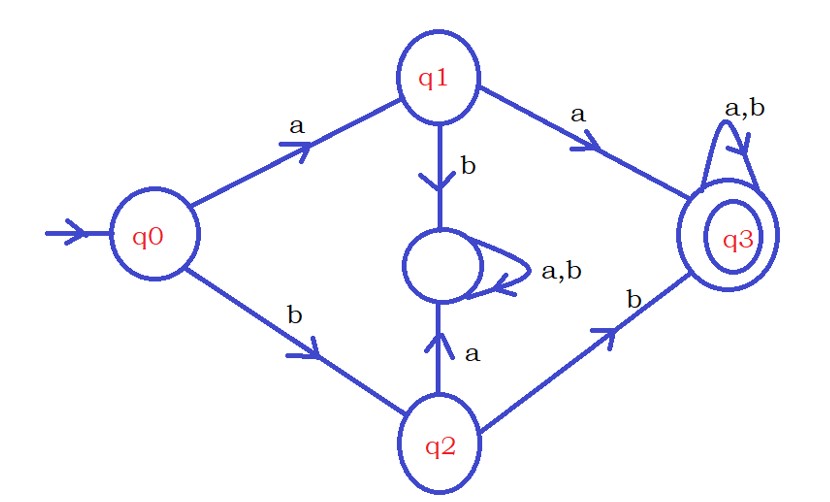
On the state q0, if we find the input character a, we are moving one side to state q1.
If we find the input character b, we are moving the other side to state q2.
On the state q1, if we encounter the input character b, we move to the dead state because we lost condition aa.
No need to check the remaining input characters. So we move to a dead state.
Similarly, on the state q2, if we encounter the input character a, we move to the dead state.
On state q1, if we encounter the input character a, we move to the final state q3 because the condition required is satisfied.
Similarly, on the state q2, if we encounter the input character b, we move to the final state q3.
Once we reach the final state, we stay on the final state for any input character.
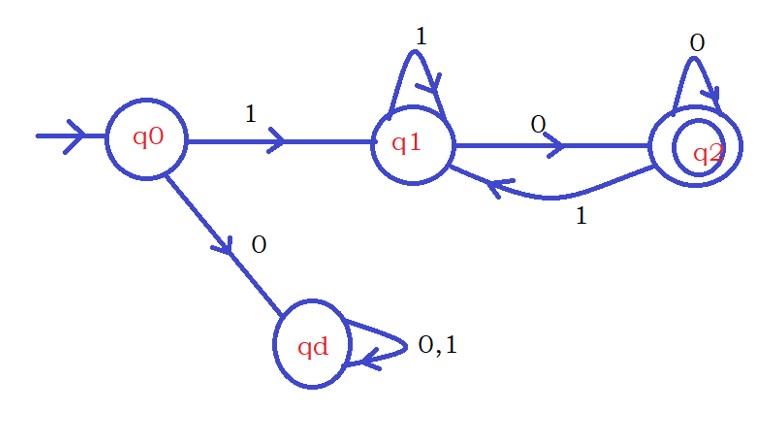
Second Question: Design DFA that accepts strings that start with 1 and ends with zero.
The input symbols are Σ {0,1}.
In our example, we need to check starting symbol 1 and the ending character zero.
Two conditions have to be checked. And both the conditions have to be satisfied.
Check the diagram below; we check the first condition and then the second condition because both should be satisfied.
Point to understand: how DFA is constructed if both the conditions are to be satisfied.
On state q0, if we encounter the input character 1, we move to state q1.
Otherwise, we move to a dead state because the first condition is lost.
We have to satisfy both the conditions, so we move to a dead state.
If the first condition is satisfied, then we construct DFA for the second condition.
On the state q1, if we encounter the input character 0, we move to state q2.
We consider state q2 the final state because we move to state q2 when both conditions are satisfied.
On state q1, if we see the input character 1, we stay on q1.
On q2, if we encounter the input character 1, we move back to state q1 because the last character is not zero.
If we see the input character 0 on state q2, we stay in the same state because the last character seen is zero.
The below diagram shows the complete DFA.