DFA with Multiple Final States

For Complete YouTube Video: Click Here

In this class, We discuss DFA with Multiple Final States.

The reader should have prior knowledge of Previous examples. Click here.

We are going step by step according to the complexity of the DFA design. So previous classes are important to understand.

First Question: Design DFA that accepts strings containing the last two characters 00 or 11.

The input symbols are Σ {0,1}.

The below diagram shows the base logic to construct the DFA.

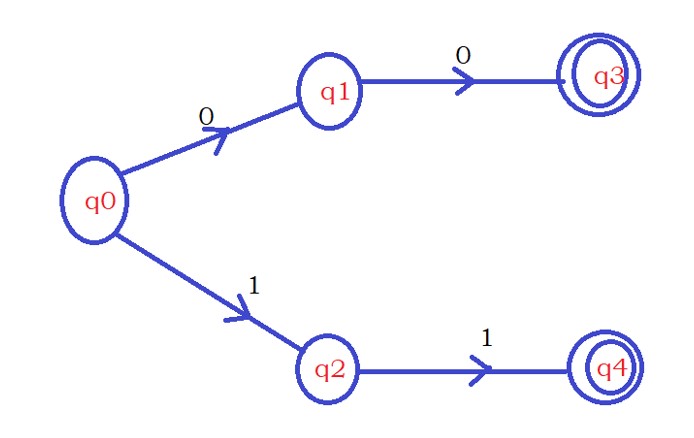
We started at q0 and moved to state q3 after seeing two zero’s.

We started at q0 and moved to state q4 after seeing two ones.

The states q3 and q4 are considered final states. This base logic understanding comes from previous examples.

Now construct the remaining logic.

The below example shows the Complete DFA.

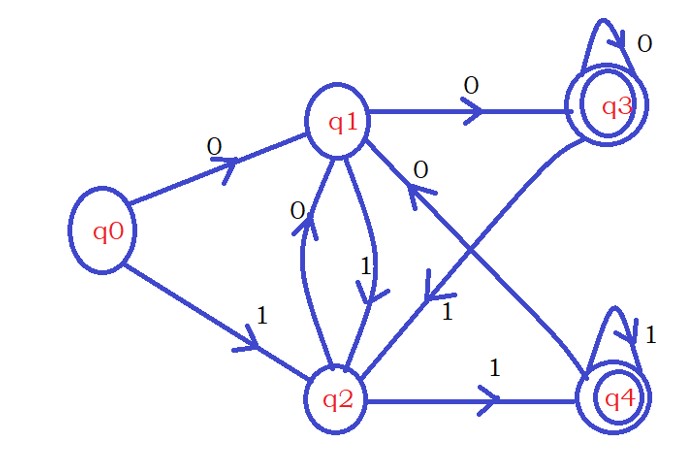
On the state q1, if we encounter the input character one, we move to state q2 because the two consecutive zeros condition is lost.

The present input character 1 fulfills half condition of two consecutive ones. so we move to the q2 state.

Similarly, on state q2, if we encounter the input character 0, we move to state q1.

On the state q3, if we see the input character 1, we move to state q2 because the last two zero characters condition is lost.

Similarly, on the state q4, if we encounter the input character 0, we move to state q1.

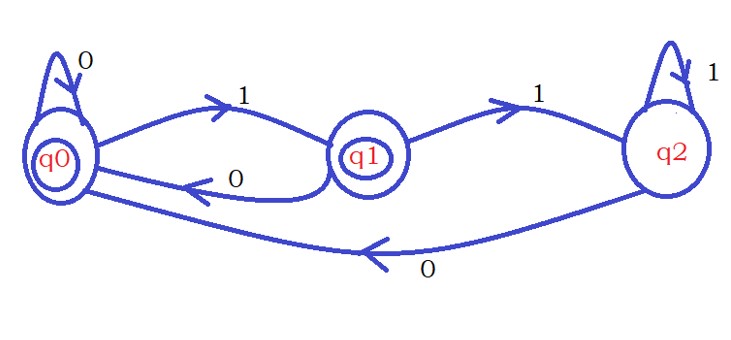
Second Question: Design DFA that accepts strings that do not have the last two characters 11.

In our previous examples, we have already designed the DFA that accepts strings having the last two characters 11.

The below diagram shows the DFA accepting the last two characters 11.

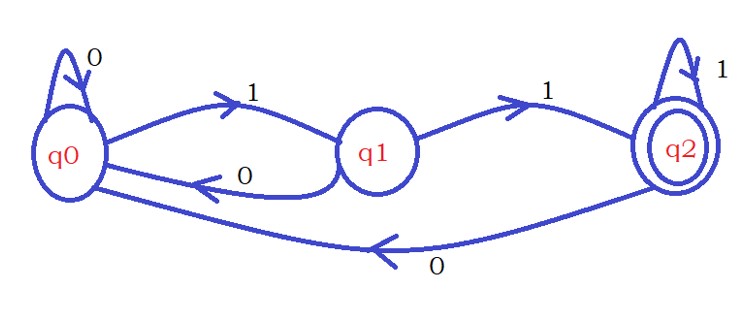
The same DFA can be modified to accept strings that do not have the last two characters 11.

Change the non-final states to final states. and final states to non-final states.

To understand the above point, we have chosen this example.

The below diagram shows the modified DFA.