Eliminating Left Recursive Grammar

In this class, We discuss Eliminating Left Recursive Grammar.

For Complete YouTube Video: Click Here

The reader should have prior knowledge of grammar expansion. Click here.

First, we understand what is left recursive grammar.

Example:

A – Aa | b

The above grammar is left recursive grammar.

The production A is called A in the first place. This type of grammar we call left recursive grammar.

The above left recursive grammar will accept the strings containing start symbol a and followed by b’s.

Take input string abbbb.

The below diagram shows the derivation tree for the input string abbbb.

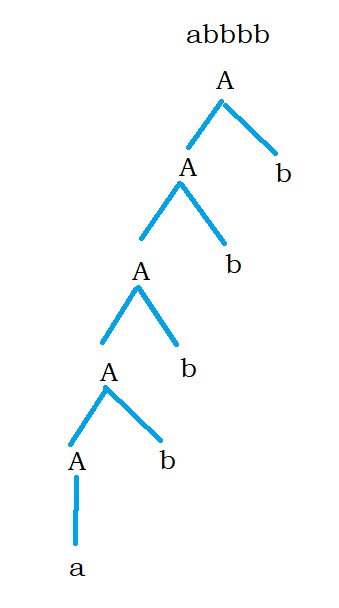
It’s expanding like A expands A, and again A expands A, and so on.

The confusion with left recursive grammar is where to stop?

The above reason why left recursive grammar is not needed.

We can convert the left recursive grammar to CFG without left recursion.

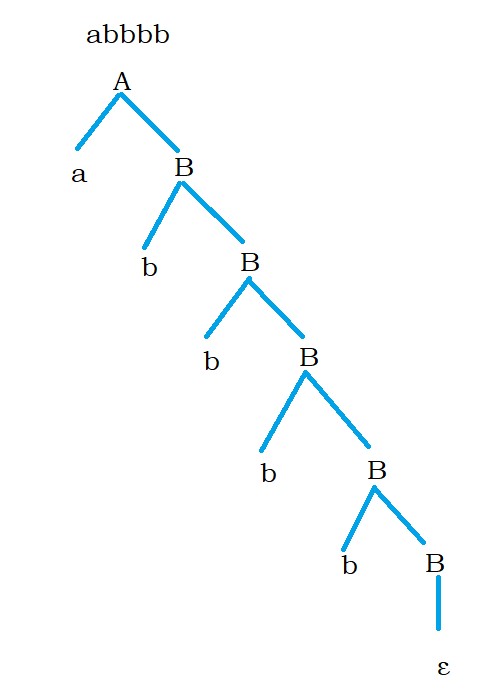
The below grammar shows that the CFG that accepts the language starts with a and then b’s. without left recursion.

A – aB

B – bB | ε

The below diagram shows the derivation tree for the input string abbbb.

The left recursive grammar is not used in top-down parsing in compiler design.

Remember the point. The reader will get clarity in the compiler design course.

How to eliminate the given left recursive grammar?

The left recursive grammar is of the form A – Aα | β

given below the left recursive grammar conversion.

A – βA’

A’ – αA’ | ε

A’ is a new nonterminal, and we can take any nonterminal name.

For better understanding, we consider A’.

Take the previous example.

A – Aa | b. Here α = a and β = b.

The left recursive grammar can be written as follows.

A – aA’

A’ – bA’ | ε