Failure Case of Finite Automata

For Complete YouTube Video: Click Here

In this class, We discuss the Failure Case of Finite Automata.

The reader should have prior knowledge of finite automata. Click Here.

Take an example alphabet Σ = {a,b}

Using the given alphabet, we can generate an infinite number of languages.

Given below are some of the languages.

L1 = { set of strings contain last two characters aa}

L2 = { set of strings contain aa as substring}

L3 = (aⁿbⁿ where n >= 0}

Like the above languages, we can write infinite using the given alphabet.

In the above languages, L1 and L2, we constructed finite automata.

For the language L3, we are not able to construct finite automata. Why?

We need to understand why we are not able to construct finite automata for L3.

Understand the language L3.

If we take n = 0, we get epsilon.

If n = 1 we get ab.

If n = 2 we get aabb. two a’s followed by two b’s.

Similarly, n = 3 we get aaabbb.

L3 = {ε, ab, aabb, aaabbb, . . . }

First, we understand an example, and then we go and discuss why we can not write finite automata for L3.

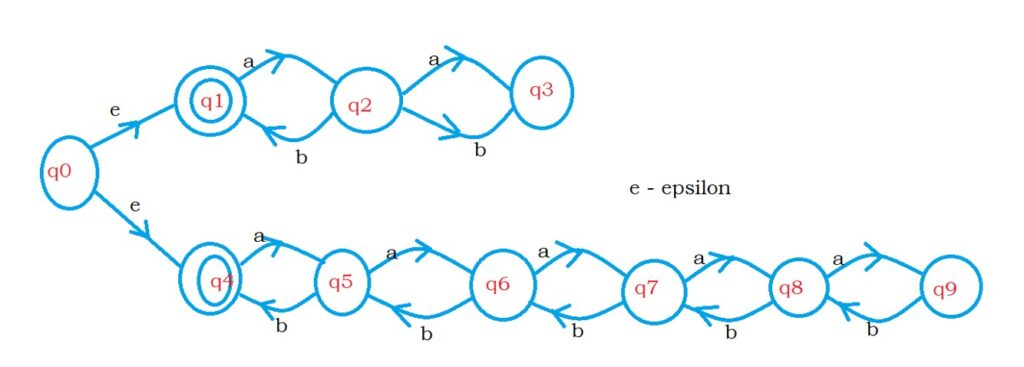
L= { ε, aaaaabbbbb}

We can construct finite automata for language L. because Language L has a finite set of strings.

The below diagram shows the finite automata for language L.

Take one more example.

L5 = { ε, aabb, aaaaabbbbb}

In the language L5, we have two a’s followed by two b’s and five a’s followed by five b’s.

The below diagram shows the finite automata for language L5.

The language L3 has infinite strings.

We need to remember the number of a’s obtained.

From our first classes, we learned finite automata do not have memory.

To maintain the count of occurrences of a’s, we need memory.

So, we can not construct DFA for the language L3.

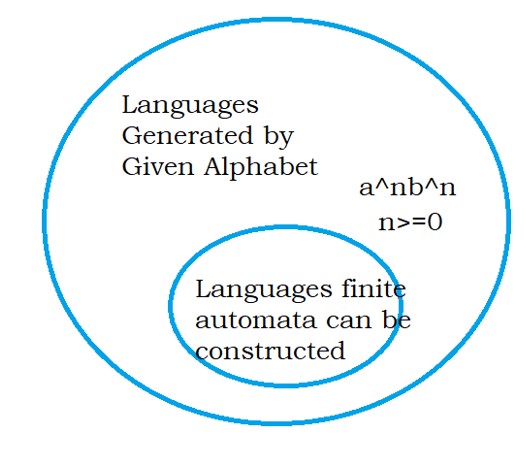
The below diagram shows the Venn diagram representation of languages.

Assume alphabet Σ = {a,b}

The outer circle represents the languages represented using the alphabet Σ = {a,b}.

Out of those, we can write finite automata for a few languages.

The inner-circle shows the set of languages in which we can construct finite automata.

One of the languages for which we can not construct finite automata is aⁿbⁿ.