Failure Case of Push Down Automata

In this class, We discuss the Failure Case of Push Down Automata.

For Complete YouTube Video: Click Here

The reader should have prior knowledge of push-down automata. Click Here.

We take an example and understand the failure case.

Example: L = aⁿbⁿcⁿ where n > 0.

The language L = {abc, aabbcc, . . .}

We can construct push-down automata for the language aⁿbⁿ.

We can not construct push-down automata for the language aⁿbⁿcⁿ. Why?

Whenever we see the input symbol a, we push on to the stack.

Whenever we see the input symbol b, we pop a from the stack.

For each b, we pop an a from the stack.

Now, we do not have a chance to count the equivalence of the symbol c.

Push down automata has only stack memory. We can count the equivalence of two symbols.

We can not construct context-free grammar for the language L. Why?

We provide an intuition why we can not construct context-free grammar for language L.

S – aSb | ε

The above grammar defines the language aⁿbⁿ.

The grammar works as explained below.

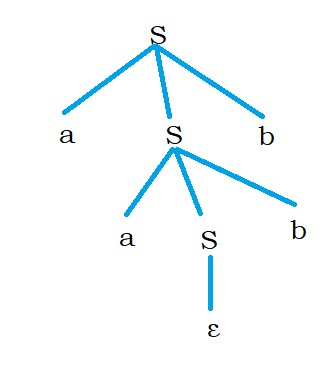
For every input symbol, a, the production S will check for symbol b.

For two a’s, the grammar will check for two b’s,

Checking equivalence for three symbols is not possible.

S – aSbSc | ε

The below derivation shows after checking b, and the production is again looking for a.

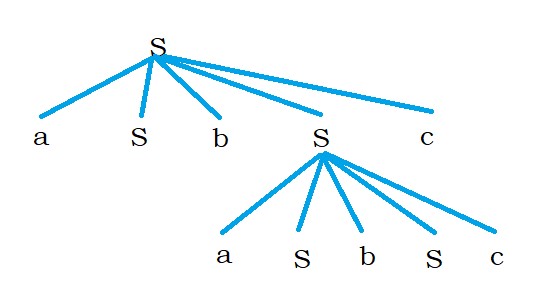
Three symbols equivalence is not possible.

The reader can try different possibilities to write CFG for the language aⁿbⁿcⁿ.

Writing CFG for the language aⁿbⁿcⁿ is not possible.