Finite Automata to Right and Left Linear Grammar

For Complete YouTube Video: Click Here

In this class, We discuss Finite Automata to Right and Left Linear Grammar.

The reader should have prior knowledge of right and left linear grammar. Click Here.

The below diagram is the finite automata we consider.

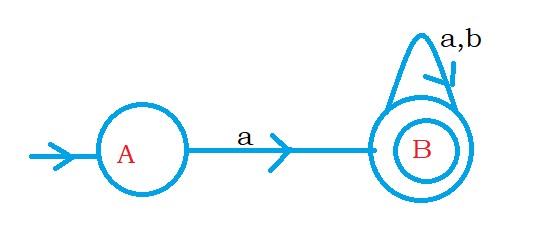
The language accepted by the finite automata is a set of strings starting with a.

Convert finite automata to the right linear grammar.

On state A if we apply input symbol a, we move to state B. written as 

A – aB.

Similarly, write for all the states.

In-state B, if we apply input symbol a, we move to state B. written as 

B – aB

In-state B, if we apply input symbol b, we move to state B. written as 

B – bB

As state B is the final state, we add an epsilon production. Because on the final state, the string is accepted.

The below-shown grammar is the final right linear grammar.

A – aB

B – aB | bB | ε

Now we need to eliminate epsilon.

Substitute epsilon in B and write the productions.

A – aB | a. after substituting epsilon, we get extra production A – a.

B – aB | bB | a | b

Now we reverse the right linear grammar.

A – aB if reversed, we get A – Ba.

Similarly, write all the productions in the right linear grammar.

The below grammar shows after reversing the right linear grammar.

A – Ba | a

B – Ba | Bb | a | b

The above grammar follows left linear grammar conditions.

The above-left linear grammar will accept the reverse of the language given.

The left linear grammar accepts strings whose last character is a.

To get the left linear grammar for language accepting strings, start with a. we reverse the finite automata and write right linear grammar and then reverse the grammar.

The below diagram shows the reverse of the finite automata.

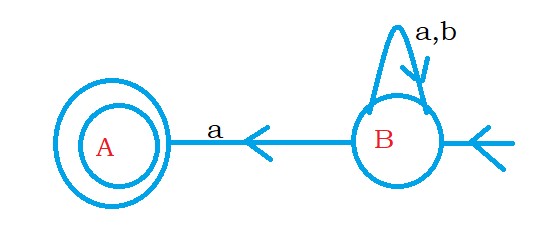
The below grammar is the right linear grammar for the reverse of finite automata.

We have to reverse the above right linear grammar.

The below grammar is left linear grammar for the given finite automata.