Finite Automata to Right and Left Linear Grammar Practice Example

For Complete YouTube Video: Click Here

In this class, We discuss Finite Automata to Right and Left Linear Grammar Practice Example.

The reader should have prior knowledge of how to convert finite automata to the right and left linear grammar. Click Here.

The below diagram shows the finite automata.

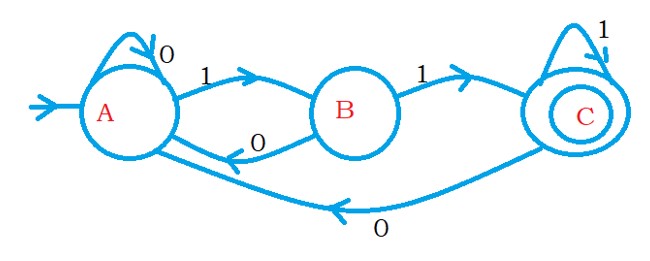
The finite automata accept the strings containing the last two characters 11.

The below shows the right linear grammar for the finite automata.

On state A if we apply input symbol 0, we move to state A. written as A – 0A.

Similarly, write for all the states.

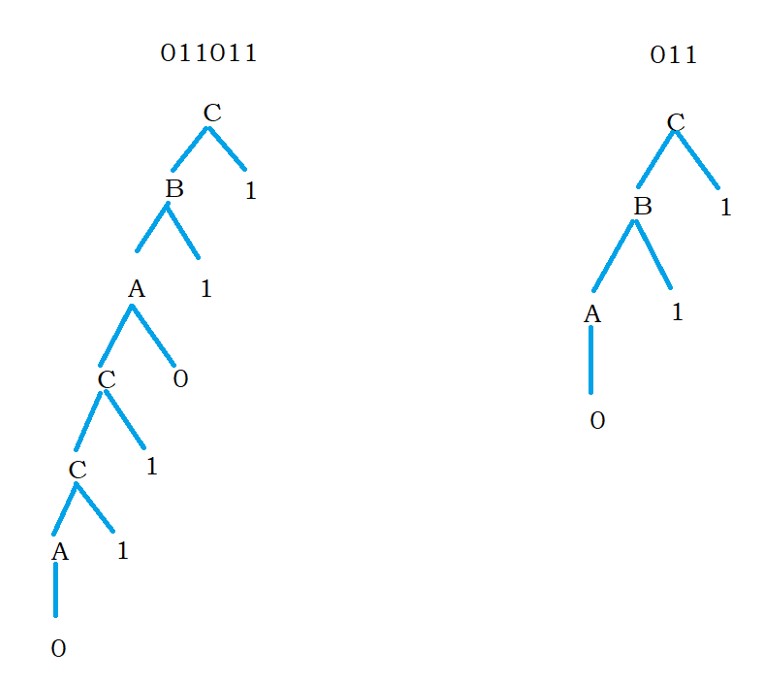
A – 0A | 1B

B – 0A | 1C

C – 0A | 1C | ε

For the final state, we add epsilon production

The below grammar is right linear grammar after eliminating epsilon production.

A – 0A | 1B

B – 0A | 1C | 1 after substituting epsilon in C, we get 1. So one is added as a new production.

C – 0A | 1C | 1

The below diagram shows the acceptance of strings by right linear grammar.

To identify left linear grammar. We need to reverse the finite automata and write the right linear grammar and reverse the grammar.

The below diagram shows the reverse of the finite automata.

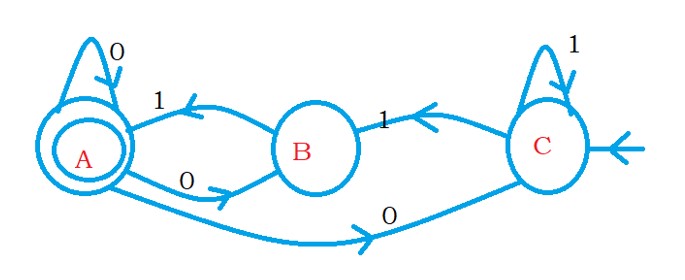
How to reverse the given finite automata? Click Here.

The below grammar shows the right linear grammar for the reverse finite automata.

C – 1C | 1B

B – 1A

A – 0A | 0C | 0B | ε

The below grammar shows right linear grammar after eliminating epsilon

C – 1C | 1B

B – 1A | 1

A – 0A | 0C | 0B | 0

The above grammar is reversed to get left linear grammar.

Below is the left linear grammar for the given finite automata.

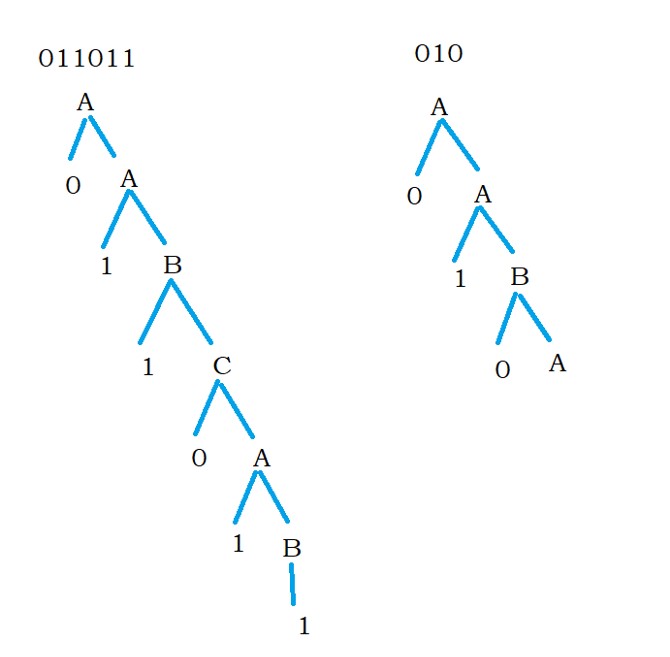
C – C1 | B1

B – A1 | 1

A – A0 | C0 | B0 | 0

The below diagram shows the acceptance of string using the left linear grammar.