Gate Bits FA and RE 4

In this class, We discuss Gate Bits FA and RE 4

For Complete YouTube Video: Click Here

The reader should have prior knowledge of finite automata and regular expressions. Click Here.

Example 1:

Gate 2003:

The regular expression 0*(10*)* denotes the same set as

(A) (1*0)*1*

(B) 0 + (0 + 10)*

(C) (0 + 1)* 10(0 + 1)*

(D) none of these

Answer: A

Check the identity rules of regular expressions. Click Here.

(a+b)* = (a*b*)* = (a*+b*)* = (a*+b)* = a*(ba*)*= (b*a)*b* from identity rules.

The given expression is equivalent to option A.

Suppose you are not good at remembering the rules. We need to check the equivalence by some sample inputs.

The input string 11 is not generated by options B and C.

Whatever strings are generated by given expressions. The same inputs can be generated using option A.

Example 2:

Gate 2017:

Let δ denote the transition function, and ˆδ denote the extended transition function of the ϵ-NFA, whose transition table is given below:

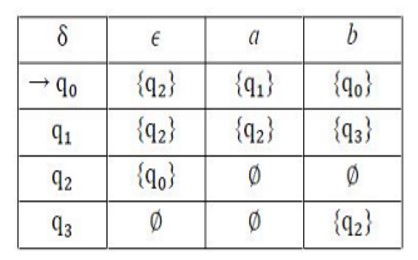
Then ˆδ(q2,aba) is

(A) ∅

(B) {q0,q1,q3}

(C) {q0,q1,q2}

(D) {q0,q2,q3}

Answer C

Click on the above video link for a complete explanation.

We need to find the epsilon closure and process the given input string.