Gate Bits FA and RE 6
In this class, We discuss Gate Bits FA and RE 6.
For Complete YouTube Video: Click Here
The reader should have prior knowledge of finite automata and regular expressions. Click Here.
Example 1:
Gate 2001:
Consider a DFA over ∑ = {a, b} accepting all strings which have number of a’s divisible by 6 and number of b’s divisible by 8. What is the minimum number of states that the DFA will have?
(A) 8
(B) 14
(C) 15
(D) 48
Answer: D
The similar example we discussed in our previous classes. Click Here.
We will have 48 states in the minimum DFA.
Example 2:
Gate 2002:
The Finite state machine described by the following state diagram with A as starting state, where an arc label is x / y and x stands for 1-bit input and y stands for 2- bit output
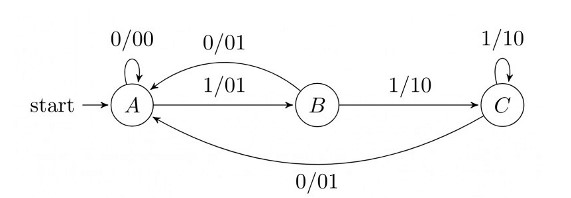
(A) Outputs the sum of the present and the previous bits of the input
(B) Outputs 01 whenever the input sequence contains 11.
(C) Outputs 00 whenever the input sequence contains 10.
(D) None of these
Answer: A
Check the outputs
Take input symbol zero.
On state A if the input symbol is 0 we move to state A and display 00.
Take input symbol 1
On state A if we take input symbol 1 we move to state Ba and display 01.
The output displayed is 01 which is binray value of present input and previous input.
The previous input is not there so considered as zero.
Take input symbol 11
On applying input symbol 11 we move to state C and the output displayed is 10.
The output 10 is binary value of 2. The present and previous symbol is 11.
1 + 1 we get 2.
Answer A matches the given finite automata.
