Grammar TOC

For Complete YouTube Video: Click Here

In this class, We discuss Grammar TOC.

The reader should have prior knowledge of finite automata and regular expressions. Click Here.

Grammar: Grammar is another way to represent a language.

To represent a language, we use finite automata or regular expressions.

One more way to represent a language is using Grammar.

A grammar is represented using four tuples.

G = {V, T, P, S}

V means set of variables. We call them nonterminals.

T means set of terminals

P means set of productions

S is the start symbol

Take an example and understand Grammar.

Language L = {set of strings containing last two characters as 11}

The below diagram shows the DFA for the language L.

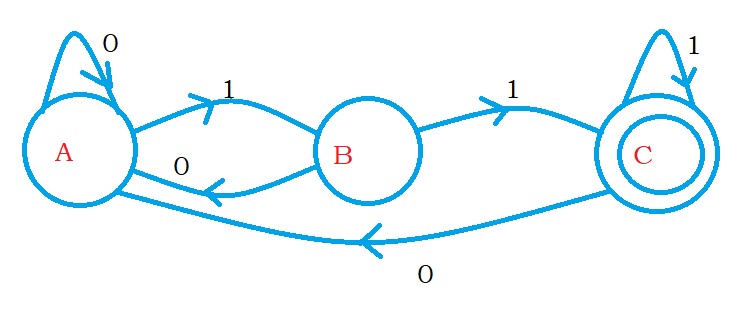
The other way to represent L is using Grammar.

V = {A,B,C} These are the non terminals.

From the above DFA, these A, B, C are states.

T = {0,1} the set of input symbols.

Given below are the productions.

A – 0A | 1B

B – 0A | 1C

C – 0A | 1C | ε

Grammar looks like the above productions.

How do we write this Grammar? We understand in our next classes.

The start symbol is A.

The programmatic intuition we provide below will help you a lot in understanding the next classes.

For the understanding purpose, we are explaining the program approach.

Take the production A – 0A | 1B.

A will check the input symbol zero and call A, or it has to check the input symbol one and call B.

For each nonterminal, we write a function.

The below are the functions for A, B, and C.

The above functions should accept the strings containing the last two characters as 11.

Start from function A.

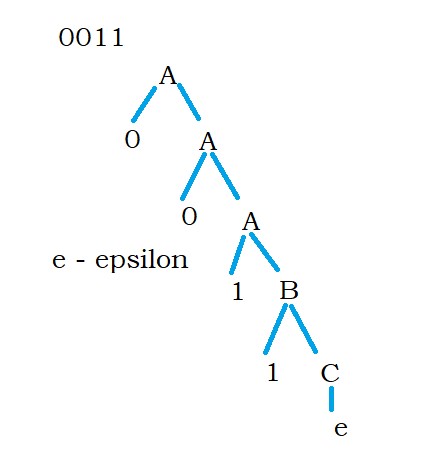
take input string 011.

In function A, take the first input character i.e., 0.

If the input character is zero, call function A.

In the second function call of A, we take the second input character.

The second input character is one, so call function B.

In function B, take the third input character.

The third input character is 1. so call function C.

In function C, the next input character is ε., so the input string is accepted.

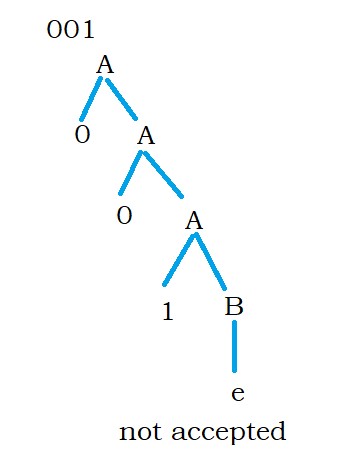
Similarly, take example string 001.

The above functions will display not accepted for the string 001.

Given below is the other way to represent the execution.

Start from A.

A will check input symbol zero and call A.

We are expanding A again.

A is called nonterminal because we are expanding.

0,1 are terminal because we are not expanding.

Similarly, expand for remaining.

Finally, C is taking epsilon to stop and accept the string. Because in the production, C is taking epsilon.

The other input string is 001. The final nonterminal is B.

Production B is not accepting epsilon, so the string is not accepted.

The tree mentioned above structure is followed in our books.

For understanding, we explained in the program.

We take one more example.

Example 2:

A – B0 | 1

B – B0 | 1

The right side of the Grammar has nonterminals on the left-hand side.

How does the above Grammar expand?

The below diagram shows the grammar expansion.

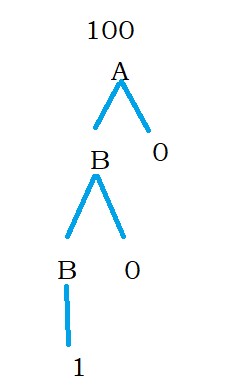
Production A has two options.

We can choose B0 or 1.

In our example, we have chosen B0.

Now expand B. Production B has two options, either B0 or 1.

We have chosen B0.

Again expand B. here, we chose to take input character 1.

The first input character is checked at last B.

After that, the input character zero is checked. Then the last input character is zero.

With the above intuition, we can easily write Grammar for a given language.